
题目列表(包括答案和解析)
2.(2009浙江理)对于正实数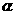 ,记
,记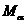 为满足下述条件的函数
为满足下述条件的函数 构成的集合:
构成的集合: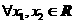 且
且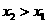 ,有
,有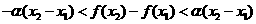 .下列结论中正确的是 ( )
.下列结论中正确的是 ( )
A.若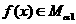 ,
,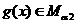 ,则
,则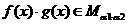
B.若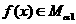 ,
,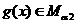 ,且
,且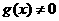 ,则
,则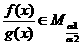
C.若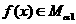 ,
,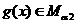 ,则
,则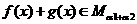
D.若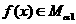 ,
,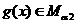 ,且
,且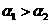 ,则
,则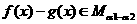
答案 C
解析 对于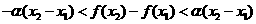 ,即有
,即有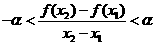 ,令
,令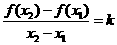 ,有
,有 ,不妨设
,不妨设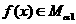 ,
,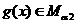 ,即有
,即有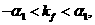
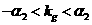 ,因此有
,因此有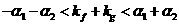 ,因此有
,因此有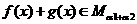 .
.
1.(2009全国卷Ⅰ理)函数 的定义域为R,若
的定义域为R,若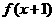 与
与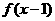 都是奇函数,则( )
都是奇函数,则( )
A. 是偶函数 B.
是偶函数 B. 是奇函数
是奇函数
C.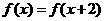 D.
D.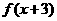 是奇函数
是奇函数
答案 D
解析 
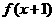 与
与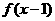 都是奇函数,
都是奇函数,
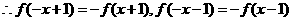 ,
,
 函数
函数 关于点
关于点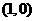 ,及点
,及点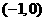 对称,函数
对称,函数 是周期
是周期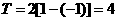 的周期函数.
的周期函数.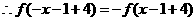 ,
,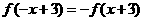 ,即
,即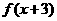 是奇函数。故选D
是奇函数。故选D
2.(2010北京文)(20)(本小题共13分)
已知集合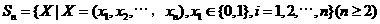 对于
对于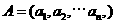 ,
,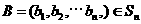 ,定义A与B的差为
,定义A与B的差为
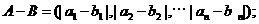
A与B之间的距离为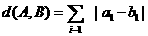
(Ⅰ)当n=5时,设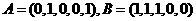 ,求
,求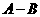 ,
,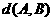 ;
;
(Ⅱ)证明: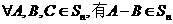 ,且
,且 ;
;
(Ⅲ) 证明: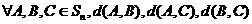 三个数中至少有一个是偶数
三个数中至少有一个是偶数
(Ⅰ)解: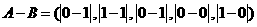 =(1,0,1,0,1)
=(1,0,1,0,1)
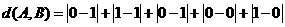 =3
=3
(Ⅱ)证明:设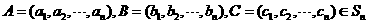
因为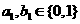 ,所以
,所以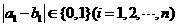
从而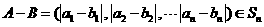
由题意知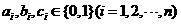
当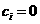 时,
时,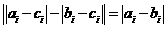
当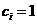 时,
时,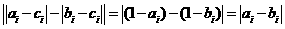
所以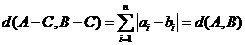
(Ⅲ)证明:设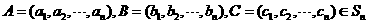
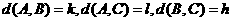
记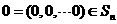 由(Ⅱ)可知
由(Ⅱ)可知
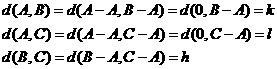
所以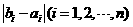 中1的个数为k,
中1的个数为k,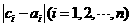 中1的个数为
中1的个数为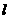
设 是使
是使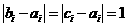 成立的
成立的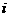 的个数。则
的个数。则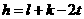
由此可知,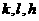 三个数不可能都是奇数
三个数不可能都是奇数
即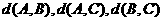 三个数中至少有一个是偶数。
三个数中至少有一个是偶数。
2009年高考题
1.(2010上海文)22.(本题满分16分)本题共有3个小题,第1小题满分3分,第2小题满分5分,第3小题满分8分。
若实数 、
、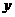 、
、 满足
满足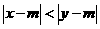 ,则称
,则称 比
比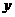 接近
接近 .
.
(1)若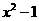 比3接近0,求
比3接近0,求 的取值范围;
的取值范围;
(2)对任意两个不相等的正数 、
、 ,证明:
,证明: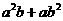 比
比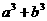 接近
接近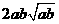 ;
;
(3)已知函数 的定义域
的定义域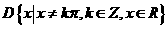 .任取
.任取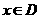 ,
, 等于
等于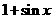 和
和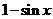 中接近0的那个值.写出函数
中接近0的那个值.写出函数 的解析式,并指出它的奇偶性、最小正周期、最小值和单调性(结论不要求证明).
的解析式,并指出它的奇偶性、最小正周期、最小值和单调性(结论不要求证明).
解析:(1) xÎ(-2,2);
(2) 对任意两个不相等的正数a、b,有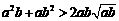 ,
,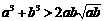 ,
因为
,
因为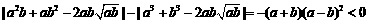 ,
所以
,
所以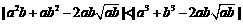 ,即a2b+ab2比a3+b3接近
,即a2b+ab2比a3+b3接近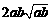 ;
(3)
;
(3) 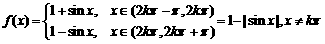 ,kÎZ,
f(x)是偶函数,f(x)是周期函数,最小正周期T=p,函数f(x)的最小值为0,
函数f(x)在区间
,kÎZ,
f(x)是偶函数,f(x)是周期函数,最小正周期T=p,函数f(x)的最小值为0,
函数f(x)在区间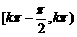 单调递增,在区间
单调递增,在区间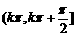 单调递减,kÎZ.
单调递减,kÎZ.
5.(2010江苏卷)5、设函数f(x)=x(ex+ae-x)(x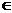 R)是偶函数,则实数a=________________
R)是偶函数,则实数a=________________
答案 a=-1
[解析]考查函数的奇偶性的知识。g(x)=ex+ae-x为奇函数,由g(0)=0,得a=-1。
4.(2010福建理)15.已知定义域为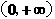 的函数
的函数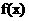 满足:①对任意
满足:①对任意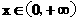 ,恒有
,恒有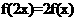 成立;当
成立;当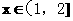 时,
时,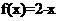 。给出如下结论:
。给出如下结论:
①对任意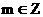 ,有
,有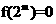 ;②函数
;②函数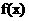 的值域为
的值域为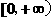 ;③存在
;③存在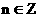 ,使得
,使得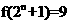 ;④“函数
;④“函数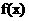 在区间
在区间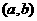 上单调递减”的充要条件是
“存在
上单调递减”的充要条件是
“存在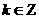 ,使得
,使得
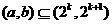 ”。
”。
其中所有正确结论的序号是 。
[答案]①②④
[解析]对①,因为 ,所以
,所以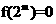 ,故①正确;经分析,容易得出②④也正确。
,故①正确;经分析,容易得出②④也正确。
[命题意图]本题考查函数的性质与充要条件,熟练基础知识是解答好本题的关键。
3.(2010全国卷1理)(15)直线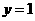 与曲线
与曲线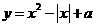 有四个交点,则
有四个交点,则 的取值范围是
.
的取值范围是
.

2.(2010广东理)9. 函数 =lg(
=lg( -2)的定义域是
.
-2)的定义域是
.
答案(1,+∞) .
[解析]∵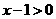 ,∴
,∴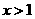 .
.
1.(2010重庆文数)(12)已知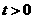 ,则函数
,则函数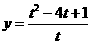 的最小值为____________ .
的最小值为____________ .
答案 -2
解析: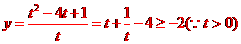 ,当且仅当
,当且仅当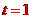 时,
时,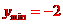
17.(2010重庆文数)(4)函数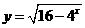 的值域是
的值域是
(A)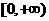 (B)
(B)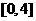
(C)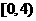 (D)
(D)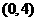
答案 B
解析: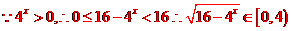
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com