
题目列表(包括答案和解析)
8.(本小题满分12分)
如图,直三棱柱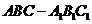 中,
中, 、
、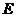 分别为
分别为 、
、 的中点,
的中点, 平面
平面
(I)证明: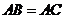
(II)设二面角 为60°,求
为60°,求 与平面
与平面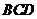 所成的角的大小。
所成的角的大小。
分析一:求 与平面
与平面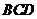 所成的线面角,只需求点
所成的线面角,只需求点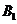 到面
到面 的距离即可。
的距离即可。
17.解析:(1)在如图,以D为坐标原点,建立空间直角坐标
依题意,得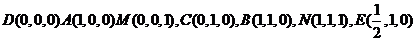 。
。

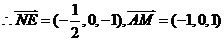
 ,
,
所以异面直线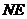 与
与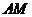 所成角的余弦值为
所成角的余弦值为 .A
.A
(2)假设在线段 上存在点
上存在点 ,使得
,使得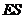
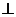 平面
平面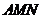 .
.
 ,
,
可设
又 .
.
由 平面
平面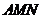 ,得
,得 即
即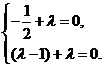
故 ,此时
,此时 .
.
经检验,当 时,
时, 平面
平面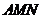 .
.
故线段 上存在点
上存在点 ,使得
,使得 平面
平面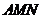 ,此时
,此时 .
.
7.(13分)
 如图,四边形ABCD是边长为1的正方形,
如图,四边形ABCD是边长为1的正方形, ,
,
 ,且MD=NB=1,E为BC的中点
,且MD=NB=1,E为BC的中点
(1) 求异面直线NE与AM所成角的余弦值
(2)
在线段AN上是否存在点S,使得ES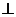 平面AMN?若存在,求线段AS的长;若不存在,请说明理由
平面AMN?若存在,求线段AS的长;若不存在,请说明理由
6.(本小题满分12分)
如图,已知两个正方行ABCD 和DCEF不在同一平面内,M,N分别为AB,DF的中点 。
(I)若平面ABCD ⊥平面DCEF,求直线MN与平面DCEF所成角的正值弦;
(II)用反证法证明:直线ME 与 BN 是两条异面直线。

设正方形ABCD,DCEF的边长为2,以D为坐标原点,分别以射线DC,DF,DA为x,y,z轴正半轴建立空间直角坐标系如图.
 则M(1,0,2),N(0,1,0),可得
则M(1,0,2),N(0,1,0),可得 =(-1,1,2).
=(-1,1,2).
又 =(0,0,2)为平面DCEF的法向量,
=(0,0,2)为平面DCEF的法向量,
可得cos(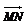 ,
, )=
)= ·
·
所以MN与平面DCEF所成角的正弦值为
cos ·
……6分
·
……6分
(Ⅱ)假设直线ME与BN共面, ……8分
则AB 平面MBEN,且平面MBEN与平面DCEF交于EN
平面MBEN,且平面MBEN与平面DCEF交于EN
由已知,两正方形不共面,故AB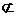 平面DCEF。
平面DCEF。
又AB//CD,所以AB//平面DCEF。面EN为平面MBEN与平面DCEF的交线,
所以AB//EN。
又AB//CD//EF,
所以EN//EF,这与EN∩EF=E矛盾,故假设不成立。
所以ME与BN不共面,它们是异面直线. ……12分
3.(本小题满分12分)
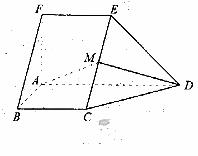 如图,在五面体ABCDEF中,FA
如图,在五面体ABCDEF中,FA 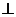 平面ABCD, AD//BC//FE,AB
平面ABCD, AD//BC//FE,AB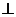 AD,M为EC的中点,AF=AB=BC=FE=
AD,M为EC的中点,AF=AB=BC=FE=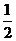 AD
AD
(I) 求异面直线BF与DE所成的角的大小;
(II)
证明平面AMD 平面CDE;
平面CDE;
(III)求二面角A-CD-E的余弦值。
如图所示,建立空间直角坐标系,
点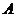 为坐标原点。设
为坐标原点。设 依题意得
依题意得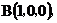

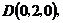



(I)
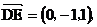

所以异面直线 与
与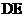 所成的角的大小为
所成的角的大小为 .
.
(II)证明:
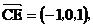
 ,
,


(III)

又由题设,平面 的一个法向量为
的一个法向量为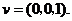


|
 平面
平面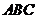 ,
,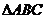
是以 为斜边的等腰直角三角形,
为斜边的等腰直角三角形, 分别为
分别为 ,
,
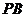 ,
, 的中点,
的中点,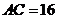 ,
,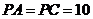 .
.
(I)设 是
是 的中点,证明:
的中点,证明: 平面
平面 ;
;
(II)证明:在 内存在一点
内存在一点 ,使
,使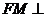 平面
平面 ,并求点
,并求点 到
到 ,
,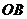 的距离.
的距离.
证明:(I)如图,连结OP,以O为坐标原点,分别以OB、OC、OP所在直线为 轴,
轴, 轴,
轴, 轴,建立空间直角坐标系O
轴,建立空间直角坐标系O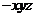 ,
,
则

 ,由题意得,
,由题意得, 因
因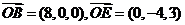 ,因此平面BOE的法向量为
,因此平面BOE的法向量为 ,
, 得
得 ,又直线
,又直线 不在平面
不在平面 内,因此有
内,因此有 平面
平面
2.在空间直角坐标系中,已知点A(1,0,2),B(1,-3,1),点M在y轴上,且M到A与到B的距离相等,则M的坐标是________。
[解析]设 由
由 可得
可得 故
故
[答案](0,-1,0)
1.若等边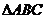 的边长为
的边长为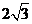 ,平面内一点
,平面内一点 满足
满足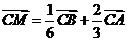 ,则
,则 _________
_________
13.(2010江苏卷)16、(本小题满分14分)
 如图,在四棱锥P-ABCD中,PD⊥平面ABCD,PD=DC=BC=1,AB=2,AB∥DC,∠BCD=900。
如图,在四棱锥P-ABCD中,PD⊥平面ABCD,PD=DC=BC=1,AB=2,AB∥DC,∠BCD=900。
(1)求证:PC⊥BC;
(2)求点A到平面PBC的距离。
[解析] 本小题主要考查直线与平面、平面与平面的位置关系,考查几何体的体积,考查空间想象能力、推理论证能力和运算能力。满分14分。
(1)证明:因为PD⊥平面ABCD,BC 平面ABCD,所以PD⊥BC。
平面ABCD,所以PD⊥BC。
由∠BCD=900,得CD⊥BC,
又PD DC=D,PD、DC
DC=D,PD、DC 平面PCD,
平面PCD,
所以BC⊥平面PCD。
因为PC 平面PCD,故PC⊥BC。
平面PCD,故PC⊥BC。
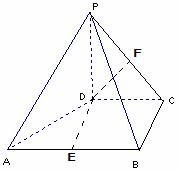 (2)(方法一)分别取AB、PC的中点E、F,连DE、DF,则:
(2)(方法一)分别取AB、PC的中点E、F,连DE、DF,则:
易证DE∥CB,DE∥平面PBC,点D、E到平面PBC的距离相等。
又点A到平面PBC的距离等于E到平面PBC的距离的2倍。
由(1)知:BC⊥平面PCD,所以平面PBC⊥平面PCD于PC,
因为PD=DC,PF=FC,所以DF⊥PC,所以DF⊥平面PBC于F。
易知DF= ,故点A到平面PBC的距离等于
,故点A到平面PBC的距离等于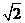 。
。
(方法二)体积法:连结AC。设点A到平面PBC的距离为h。
因为AB∥DC,∠BCD=900,所以∠ABC=900。
从而AB=2,BC=1,得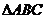 的面积
的面积 。
。
由PD⊥平面ABCD及PD=1,得三棱锥P-ABC的体积 。
。
因为PD⊥平面ABCD,DC 平面ABCD,所以PD⊥DC。
平面ABCD,所以PD⊥DC。
又PD=DC=1,所以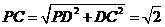 。
。
由PC⊥BC,BC=1,得 的面积
的面积 。
。
由 ,
, ,得
,得 ,
,
故点A到平面PBC的距离等于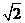 。
。
2009年高考题
12.(2010湖南理)



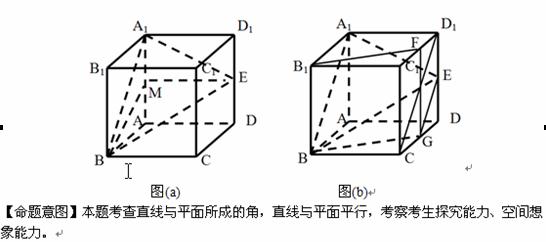
11.(2010福建文)20. (本小题满分12分)
如图,在长方体ABCD – A1B1C1D1中,E,H分别是棱A1B1,D1C1上的点(点E与B1不重合),且EH//A1D1。过EH的平面与棱BB1,CC1相交,交点分别为F,G。
 (I)证明:AD//平面EFGH;
(I)证明:AD//平面EFGH;
(II)设AB=2AA1=2a。在长方体ABCD-A1B1C1D1内随机选取一点,记该点取自于几何体A1ABFE – D1DCGH内的概率为p。当点E,F分别在棱A1B1, B1B上运动且满足EF=a时,求p的最小值。


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com