
题目列表(包括答案和解析)
5. (马鞍山学业水平测试)(本小题满分8分)
(马鞍山学业水平测试)(本小题满分8分)
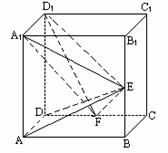
如图,在正方体ABCD-A1B1C1D1中,E、F分别是BB1、CD的中点.
(Ⅰ)证明:AD⊥D1F;
(Ⅱ)求AE与D1F所成的角;
(Ⅲ)证明:面AED⊥面A1FD1.
解:以D为原点,DA,DC,DD1为x,y,z轴建立空间直角坐标系.
设正方体的棱长为1…………………………………………………………………………1分
则有A(1,0,0),E(1,2,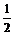 ),F(0,
),F(0,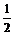 ,0),D1(0,0,1),A1(1,0,1)……2分
,0),D1(0,0,1),A1(1,0,1)……2分
(Ⅰ)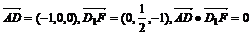 ,∴AD⊥D1F………………………4分
,∴AD⊥D1F………………………4分
(Ⅱ)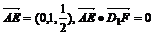 ,∴AE⊥D1F
,∴AE⊥D1F
AE与D1F所成的角为900…………………………………………………………………6分
(Ⅲ)由以上可知D1F⊥平面AED,又D1F在平面A1FD1内,
∴面AED⊥面A1FD1……………………………………………………………………8分
|
 平面
平面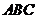 ,
,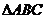
 是以
是以 为斜边的等腰直角三角形,
为斜边的等腰直角三角形, 分别为
分别为 ,
,
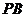 ,
, 的中点,
的中点,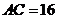 ,
,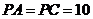 .
.
(I)设 是
是 的中点,证明:
的中点,证明: 平面
平面 ;
;
(II)证明:在 内存在一点
内存在一点 ,使
,使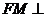 平面
平面 .
.
证明:(I)如图,连结OP,以O为坐标原点,分别以OB、OC、OP所在
直线为 轴,
轴, 轴,
轴, 轴,建立空间直角坐标系O
轴,建立空间直角坐标系O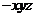 ,则
,则


 ,由题意得,
,由题意得, 因
因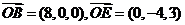 ,因此平面BOE的法向量为
,因此平面BOE的法向量为 ,
, 得
得 ,又直线
,又直线 不在平面
不在平面 内,因此有
内,因此有 平面
平面
(II)设点M的坐标为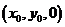 ,则
,则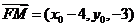 ,因为
,因为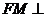 平面BOE,所以有
平面BOE,所以有 ,因此有
,因此有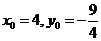 ,即点M的坐标为
,即点M的坐标为 ,在平面直角坐标系
,在平面直角坐标系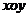 中,
中,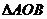 的内部区域满足不等式组
的内部区域满足不等式组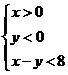 ,经检验,点M的坐标满足上述不等式组,所以在
,经检验,点M的坐标满足上述不等式组,所以在 内存在一点
内存在一点 ,使
,使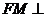 平面
平面 ,
,
4.(池州市七校元旦调研)设向量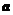 ,
,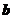 满足:
满足: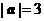 ,
,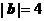 ,
,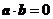 .以
.以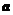 ,
,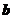 ,
, 的模为边长构成三角形,则它的边与半径为
的模为边长构成三角形,则它的边与半径为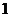 的圆的公共点个数最多为 ( )
的圆的公共点个数最多为 ( )
A. B.
B. C.
C.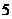 D.
D.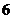
答案:C
[解析]对于半径为1的圆有一个位置是正好是三角形的内切圆,此时只有三个交点,对于圆的位置稍一右移或其他的变化,能实现4个交点的情况,但5个以上的交点不能实现.
3.(师大附中理)设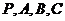 是半径为2的球面上四个不同的点,且满足
是半径为2的球面上四个不同的点,且满足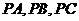 两两互相垂直,则
两两互相垂直,则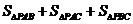 的最大值是__________。
的最大值是__________。
答案:8
2.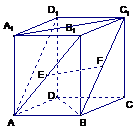 (肥城市第二次联考)如右图所示,在正方体
(肥城市第二次联考)如右图所示,在正方体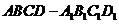 中,
中,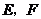 分别是
分别是
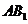 ,
, 的中点,则以下结论中不成立的是( C )
的中点,则以下结论中不成立的是( C )
A. 与
与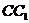 垂直 B.
垂直 B. 与
与 垂直
垂直
C. 与
与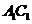 异面 D.
异面 D. 与
与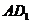 异面
异面
答案 C
解析:连结 ,在
,在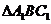 中,
中,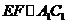 ,所以A、B、D正确,C错,选C。
,所以A、B、D正确,C错,选C。
1.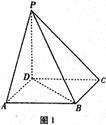 (师大附中理)如图1,
(师大附中理)如图1, 是正方形
是正方形 所在平面外一点,
所在平面外一点, 平面
平面 ,
,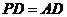 ,则
,则 与
与 所成的角的度数为
所成的角的度数为
A.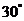 B.
B.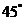
C.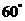 D.
D.
答案:C
2010年联考题
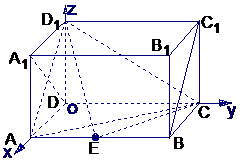
7.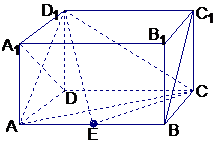 (2005江西)如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E在棱AB上移动.
(2005江西)如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E在棱AB上移动.
(1)证明:D1E⊥A1D;
(2)当E为AB的中点时,求点E到面ACD1的距离;
(3)AE等于何值时,二面角D1-EC-D的大小为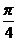 .
.
以D为坐标原点,直线DA,DC,DD1分别为x, y, z轴,建 立空间直角坐标系,设AE=x,则A1(1,0,1),D1(0,0,1),
E(1,x,0),A(1,0,0),C(0,2,0)
(1)证明 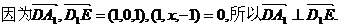
(2)解 因为E为AB的中点,则E(1,1,0),
 从而
从而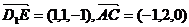 ,
,
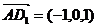 ,
,
设平面ACD1的法向量为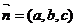 ,
,
则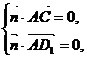
也即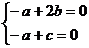 ,得
,得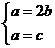 ,从而
,从而 ,所以点E到平面AD1C的距离为
,所以点E到平面AD1C的距离为
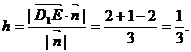
(3)解 设平面D1EC的法向量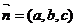 ,
,
∴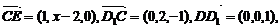
由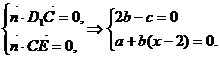 令b=1, ∴c=2,a=2-x,
令b=1, ∴c=2,a=2-x,
∴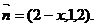
依题意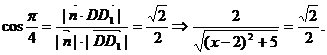
∴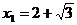 (不合,舍去),
(不合,舍去),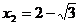 .
.
∴AE=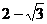 时,二面角D1-EC-D的大小为
时,二面角D1-EC-D的大小为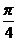 .
.
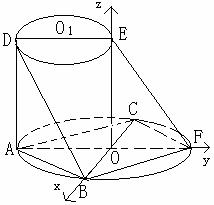
6.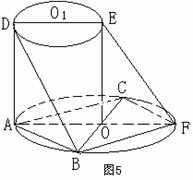 (2006广东卷)如图所示,AF、DE分别是⊙O、⊙O1的直
(2006广东卷)如图所示,AF、DE分别是⊙O、⊙O1的直
径.AD与两圆所在的平面均垂直,AD=8,BC是⊙O的直径,
AB=AC=6,OE//AD.
(Ⅰ)求二面角B-AD-F的大小;
(Ⅱ)求直线BD与EF所成的角.
解 (Ⅰ)∵AD与两圆所在的平面均垂直,
∴AD⊥AB, AD⊥AF,故∠BAD是二面角B-AD-F的平面角,
依题意可知,ABCD是正方形,所以∠BAD=450.
即二面角B-AD-F的大小为450.
(Ⅱ)以O为原点,BC、AF、OE所在直线为坐标轴,建立空间直角坐标系(如图所示),则O(0,0,0),A(0,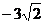 ,0),B(
,0),B(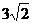 ,0,0),D(0,
,0,0),D(0,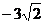 ,8),E(0,0,8),F(0,
,8),E(0,0,8),F(0,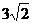 ,0)
,0)
 所以,
所以,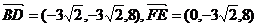
 .
.
设异面直线BD与EF所成角为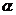 ,
,
则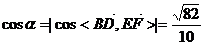
直线BD与EF所成的角为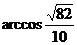
5.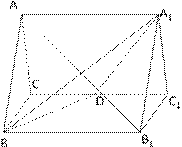 (2007福建理•18)如图,正三棱柱ABC-A1B1C1的所有
(2007福建理•18)如图,正三棱柱ABC-A1B1C1的所有
棱长都为2,D为CC1中点。
(Ⅰ)求证:AB1⊥面A1BD;
(Ⅱ)求二面角A-A1D-B的大小;
(Ⅲ)求点C到平面A1BD的距离;
(Ⅰ)证明 取 中点
中点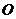 ,连结
,连结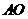 .
.
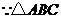 为正三角形,
为正三角形,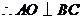 .
.
 在正三棱柱
在正三棱柱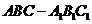 中,平面
中,平面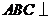 平面
平面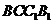 ,
,
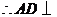 平面
平面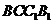 .
.
取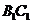 中点
中点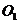 ,以
,以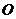 为原点,
为原点,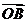 ,
, ,
,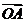 的方向为
的方向为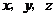 轴的正方向建立空间直角坐标系,则
轴的正方向建立空间直角坐标系,则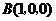 ,
,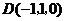 ,
,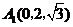 ,
,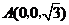 ,
,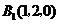 ,
,
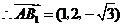 ,
, ,
,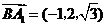 .
.
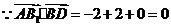 ,
,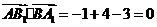 ,
,

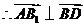 ,
,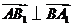 .
.
 平面
平面 .
.
(Ⅱ)解 设平面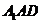 的法向量为
的法向量为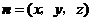 .
.
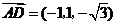 ,
,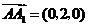 .
.
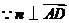 ,
,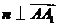 ,
,

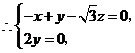
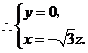
令 得
得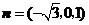 为平面
为平面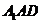 的一个法向量.
的一个法向量.
由(Ⅰ)知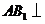 平面
平面 ,
,
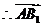 为平面
为平面 的法向量.
的法向量.
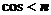 ,
,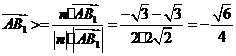 .
.
 二面角
二面角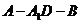 的大小为
的大小为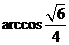 .
.
(Ⅲ)解 由(Ⅱ), 为平面
为平面 法向量,
法向量,
 .
.
 点
点 到平面
到平面 的距离
的距离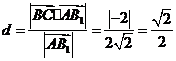 .
.
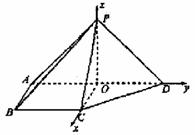
4.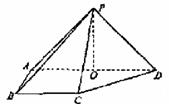 (2008福建18)如图,在四棱锥P-ABCD中,则面PAD⊥底面 ABCD,侧棱PA=PD=
(2008福建18)如图,在四棱锥P-ABCD中,则面PAD⊥底面 ABCD,侧棱PA=PD=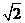 ,底面ABCD为直角梯形,
,底面ABCD为直角梯形,
其中BC∥ AD,AB⊥AD,AD=2AB=2BC=2,O为AD中点.
(Ⅰ)求证:PO⊥平面ABCD;
(Ⅱ)求异面直线PD与CD所成角的大小;
(Ⅲ)线段AD上是否存在点Q,使得它到平面PCD的距离为 ?若存在,求出
?若存在,求出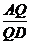 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(Ⅰ)证明 在△PAD中PA=PD,O为AD中点,所以PO⊥AD,
又侧面PAD⊥底面ABCD,平面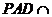 平面ABCD=AD,
平面ABCD=AD,
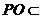 平面PAD,
平面PAD,
所以PO⊥平面ABCD.
 (Ⅱ)解 以O为坐标原点,
(Ⅱ)解 以O为坐标原点,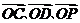 的方向分别为x轴、y轴、
的方向分别为x轴、y轴、
z轴的正方向,建立空间直角坐标系O-xyz,依题意,易得
A(0,-1,0),B(1,-1,0),C(1,0,0),D(0,1,0),P(0,0,1),
所以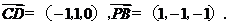
所以异面直线PB与CD所成的角是arccos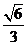 ,
,
(Ⅲ)解 假设存在点Q,使得它到平面PCD的距离为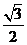 ,
,
由(Ⅱ)知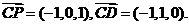
设平面PCD的法向量为n=(x0,y0,z0).
则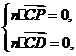 所以
所以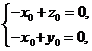 即
即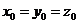 ,
,
取x0=1,得平面PCD的一个法向量为n=(1,1,1).
设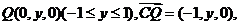 由
由 ,得
,得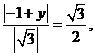
解y=-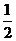 或y=
或y= (舍去),
(舍去),
此时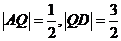 ,所以存在点Q满足题意,此时
,所以存在点Q满足题意,此时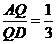 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com