
题目列表(包括答案和解析)
15. 解:以CD为x轴,CA为y轴,以CE为z轴建立空间坐标系,
(1)C(0,0,0),D(1,0,0),A(0,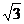 ,0),F(0,
,0),F(0,
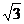 ,
,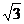 ),B(-1,
),B(-1,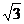 ,0),
,0),
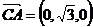 ,
,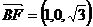 ,
,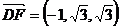 ,
,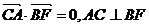
(2)平面ABD的法向量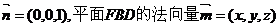
解出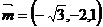 ,cos
,cos
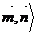 =
=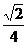 ,所求二面角F-BD-A的大小arccos
,所求二面角F-BD-A的大小arccos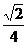
(3)点A到平面FBD的距离为d,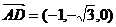
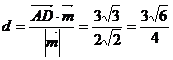 .
.
15.(本小题满分12分)
(祥云一中三次月考理)如图,已知平行四边形ABCD和矩形ACEF所在的平面互相垂直,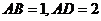 ,
,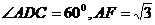 .
.
(1)求证:AC⊥BF;
(2)求二面角F-BD-A的大小;
(3) 求点A到平面FBD的距离.

14.(祥云一中三次月考文)(本小题满分12分)
 如图,已知正四棱柱
如图,已知正四棱柱 -
-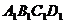 中AB=1,A
中AB=1,A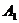 =2,N是
=2,N是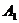 D的中点,点M在BB
D的中点,点M在BB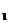 上,异面直线MN、
上,异面直线MN、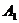 A互相垂直.
A互相垂直.
(1)试确定点M的位置,并加以证明;
(2)求二面角A-MN-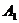 的大小.
的大小.
解:(Ⅰ)取A1A的中点P,连PM、PN,则PN//AD,
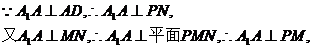
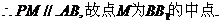
(Ⅱ)由(Ⅰ)知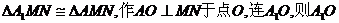 ,
,
则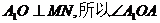 就是所求二面角的平面角.
就是所求二面角的平面角.
显然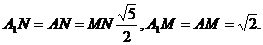
利用等面积法求得A1O=AO=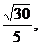 在△A1OA中由余弦定理得
在△A1OA中由余弦定理得
cos∠A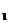 OA=
OA=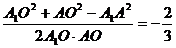
所以二面角的大小为
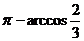
解二:(向量法) (咯)
13. 解:以CD为x轴,CA为y轴,以CE为z轴建立空间坐标系,
(1)C(0,0,0),D(1,0,0),A(0,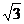 ,0),F(0,
,0),F(0,
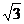 ,
,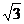 ),B(-1,
),B(-1,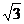 ,0),
,0),

12.(祥云一中三次月考理)(本小题满分12分)
如图,已知平行四边形ABCD和矩形ACEF所在的平面互相垂直,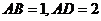 ,
,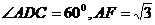 .
.
(1)求证:AC⊥BF;
(2)求二面角F-BD-A的大小.


11.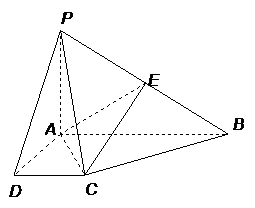 (祥云一中二次月考理)(本小题满分12分)
(祥云一中二次月考理)(本小题满分12分)
如图所示,四棱锥P-ABCD中,侧棱PA与底面ABCD垂直,DC=1,AD=AP=2,AB=5,∠CDA=∠DAB=90°,E是PB的中点.
(1)求证:BC⊥平面PAC;
(2)求异面直线PD、AE所成角的大小;
(3)求二面角A-CE-B的大小..
法一: (1)证:由题意:AC=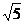 ,则
,则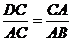 ,又∠DCA=∠CAB,所以△DCA 与△CAB
相似,所以 BC⊥AC,又由侧棱PA与底面ABCD垂直,有PA ⊥BC,
,又∠DCA=∠CAB,所以△DCA 与△CAB
相似,所以 BC⊥AC,又由侧棱PA与底面ABCD垂直,有PA ⊥BC,
所以BC⊥平面PAC;……………4分
(2)连BD,取BD的中点M,连EM,
则EM‖PD,△AEM中,AE=AM=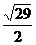 ,EM=
,EM= ,设异面直线PD、AE所成角为
,设异面直线PD、AE所成角为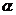 ,则
,则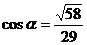 ,所以PD、AE所成角为
,所以PD、AE所成角为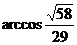 .
.
(3)作AH⊥PC于H,作HK⊥EC于K,连AK,又(1)可知.∠AKH即为所求二面角的平面角的补角.在△APC中求出AH=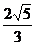 ,在△ACE中求出AK=
,在△ACE中求出AK=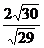 ,(或在△PCE中求出HK=
,(或在△PCE中求出HK=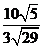 )
)
所求二面角的大小为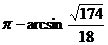 (或为
(或为 ).
).
法二:(坐标法)(2)PD、AE所成角为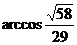 .
.
(3)所求二面角的大小为: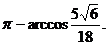
10.解:
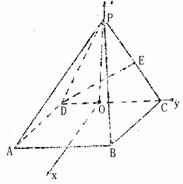 如图取DC的中点O,连PO,∵△PDC为正三角形,∴PO⊥DC.
如图取DC的中点O,连PO,∵△PDC为正三角形,∴PO⊥DC.
又∵面PDC⊥面ABCD,∴PO⊥面ABCD.如图建立空间直角坐标系
则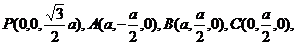
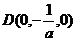
(1)E为PC中点,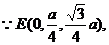
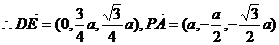 ,
,
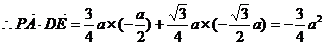 ,
,
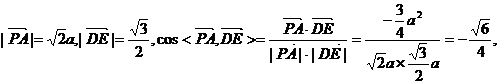
………………………………….6分
(2)可求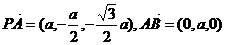 ,
,
设面PAB的一个法向量为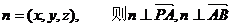 ,
,
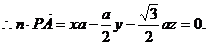 ①
① 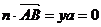 .
②
.
②
由②得y=0,代入①得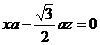 令
令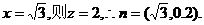
则D到面PAB的距离d等于
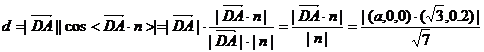
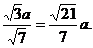 即点D到面PAB的距离等于
即点D到面PAB的距离等于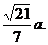 ……………………………..12分
……………………………..12分
9.(祥云一中月考理)(本小题满分12分)
如图,四棱锥P-ABCD中,底面四边形ABCD是正方形,侧面PDC是边长为a的正三角形,且平面PDC⊥底面ABCD,E为PC的中点。
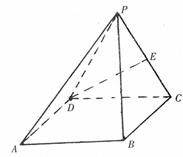 (I)求异面直线PA与DE所成的角的余弦值;
(I)求异面直线PA与DE所成的角的余弦值;
(II)求点D到面PAB的距离.
8. (玉溪一中期中文)(本小题12分)如图,在四棱锥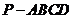 中,
中,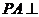 底面
底面 ,
,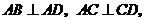
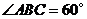 ,
,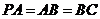 ,
,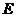 是
是 的中点.
的中点.
(Ⅰ)求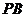 和平面
和平面 所成的角的大小;
所成的角的大小;
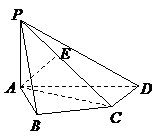 (Ⅱ)证明
(Ⅱ)证明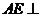 平面
平面 ;
;
(Ⅲ)求二面角 的大小.
的大小.
(Ⅰ)解:在四棱锥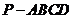 中,因
中,因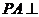 底面
底面 ,
,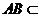 平面
平面 ,故
,故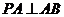 .
.
又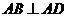 ,
,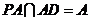 ,从而
,从而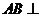 平面
平面 .故
.故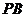 在平面
在平面 内的射影为
内的射影为 ,从而
,从而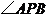 为
为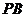 和平面
和平面 所成的角.
所成的角.
 在
在 中,
中,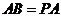 ,故
,故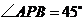 .
.
所以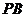 和平面
和平面 所成的角的大小为
所成的角的大小为 .
.
(Ⅱ)证明:在四棱锥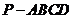 中,
中,
因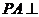 底面
底面 ,
,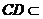 平面
平面 ,故
,故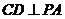 .
.
由条件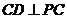 ,
,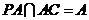 ,
,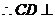 面
面 .
.
又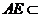 面
面 ,
,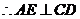 .
.
由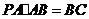 ,
,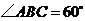 ,可得
,可得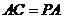 .
.
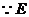 是
是 的中点,
的中点,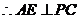 ,
,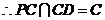 .综上得
.综上得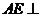 平面
平面 .
.
(Ⅲ)解:过点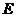 作
作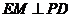 ,垂足为
,垂足为 ,连结
,连结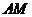 .由(Ⅱ)知,
.由(Ⅱ)知,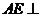 平面
平面 ,
,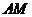 在平面
在平面 内的射影是
内的射影是 ,则
,则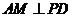 .
.
因此 是二面角
是二面角 的平面角.
的平面角.
由已知,可得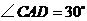 .设
.设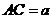 ,可得
,可得
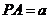 ,
,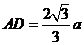 ,
,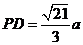 ,
, .
.
在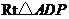 中,
中,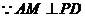 ,∴
,∴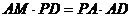 ,则
,则
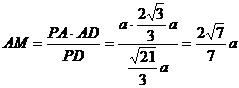 .
.
在 中,
中,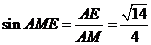 .所以二面角
.所以二面角 的大小
的大小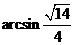
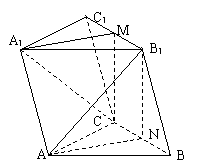
7.(马鞍山学业水平测试)(本小题满分12分)
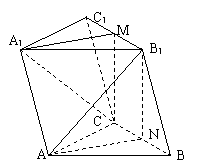 (文)在斜三棱柱
(文)在斜三棱柱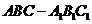 中,M为
中,M为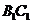 的中点,N是BC上一点.
的中点,N是BC上一点.
(Ⅰ)若平面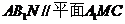 ,求证:N为BC的中点;
,求证:N为BC的中点;
(Ⅱ)在(Ⅰ)的条件下,若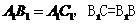 ,求证:
,求证: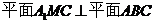 .
.
 (Ⅰ)
(Ⅰ)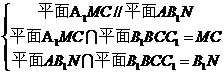 ,所以
,所以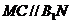
因为M为B1C1中点,所以N为BC中点----------------------6分
(Ⅱ)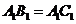 ,且M为中点,所以
,且M为中点,所以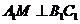 ----------8分
----------8分
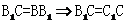 ,M为中点,所以
,M为中点,所以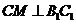 ,----------10分
,----------10分
又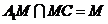 ,则
,则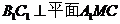 ,
----------12分
,
----------12分
又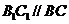 ,所以
,所以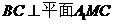 ,
----------14分
,
----------14分
又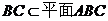 ,所以
,所以
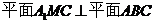 -------16分
-------16分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com