
题目列表(包括答案和解析)
5. (肥城市第二次联考)若将函数 的图像向右平移
的图像向右平移 个单位长度后,与函数
个单位长度后,与函数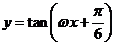 的图像重合,则
的图像重合,则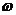 的最小值为
的最小值为
A. B.
B.
 C.
C.  D.
D.

答案 D
解析:
 ,
,
又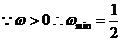 .故选D
.故选D
4.(祥云一中三次月考理)在△ABC中,角A、B、C所对的边分别为a、b、c,已知B= ,
, ,c=2,则△ABC的面积为
,c=2,则△ABC的面积为
A. B.1 C.
B.1 C.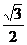 D.
D.
答案:A
3.(池州市七校元旦调研)已知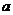 是实数,则函数
是实数,则函数 的图象不可能是 ( )
的图象不可能是 ( )

答案 D
解析 对于振幅大于1时,三角函数的周期为 ,而D不符合要求,它的振幅大于1,但周期反而大于了
,而D不符合要求,它的振幅大于1,但周期反而大于了 .
.
2.(玉溪一中期中文)已知sin =
= ,cos
,cos =
= ,则角
,则角 所在的象限是 ( )
所在的象限是 ( )
A.第一象限. B. 第二象限. C. 第三象限. D. 第四象限.
答案:B
1. (池州市七校元旦调研)如果函数 的图像关于点
的图像关于点 中心对称,那么
中心对称,那么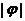 的最小值为( )
的最小值为( )
(A) (B)
(B)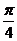 (C)
(C) (D)
(D) 
答案 A
解析: 函数
函数 的图像关于点
的图像关于点 中心对称
中心对称

 由此易得
由此易得 .故选A
.故选A
2010年联考题
题组二(5月份更新)
19.(2007江西)如图,函数 的图象与
的图象与 轴交于点
轴交于点 ,且在该点处切线的斜率为
,且在该点处切线的斜率为 .
.
 (1)求
(1)求 和
和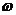 的值;
的值;
(2)已知点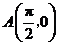 ,点
,点 是该函数图象上一点,点
是该函数图象上一点,点 是
是 的中点,当
的中点,当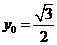 ,
, 时,求
时,求 的值.
的值.
解:(1)将 ,
, 代入函数
代入函数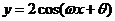 得
得 ,
,
因为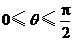 ,所以
,所以 .
.
又因为 ,
,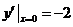 ,
, ,所以
,所以 ,
,
因此 .
.
(2)因为点 ,
, 是
是 的中点,
的中点,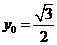 ,
,
所以点 的坐标为
的坐标为 .
.
又因为点 在
在 的图象上,所以
的图象上,所以 .
.
因为 ,所以
,所以 ,
,
从而得 或
或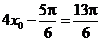 .
.
即 或
或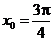 .
.
18.(2007湖北)已知函数 ,
,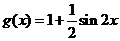 .
.
(I)设 是函数
是函数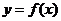 图象的一条对称轴,求
图象的一条对称轴,求 的值.
的值.
(II)求函数 的单调递增区间.
的单调递增区间.
解:(I)由题设知 .
.
因为 是函数
是函数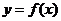 图象的一条对称轴,所以
图象的一条对称轴,所以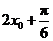
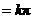 ,
,
即 (
( ).
).
所以 .
.
当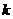 为偶数时,
为偶数时, ,
,
当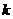 为奇数时,
为奇数时, .
.
(II)
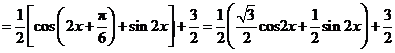
 .
.
当 ,即
,即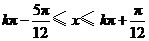 (
( )时,
)时,
函数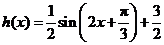 是增函数,
是增函数,
故函数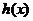 的单调递增区间是
的单调递增区间是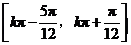 (
( ).
).
17.(2008广东)已知函数 ,
, 的最大值是1,其图像经过点
的最大值是1,其图像经过点 .
.
(1)求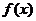 的解析式;
的解析式;
(2)已知 ,且
,且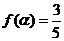 ,
, ,求
,求 的值.
的值.
解(1)依题意有 ,则
,则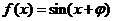 ,将点
,将点 代入得
代入得 ,
,
而 ,
, ,
, ,故
,故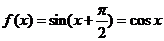 ;
;
(2)依题意有 ,而
,而 ,
,
 ,
,
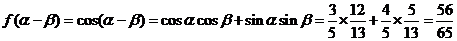
16.(2008山东)已知函数f(x)= 为偶函数,且函数y=f(x)图象的两相邻对称轴间的距离为
为偶函数,且函数y=f(x)图象的两相邻对称轴间的距离为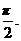
(Ⅰ)求f( )的值;
)的值;
(Ⅱ)将函数y=f(x)的图象向右平移 个单位后,再将得到的图象上各点的横坐标伸长到原来的4倍,纵坐标不变,得到函数y=g(x)的图象,求g(x)的单调递减区间.
个单位后,再将得到的图象上各点的横坐标伸长到原来的4倍,纵坐标不变,得到函数y=g(x)的图象,求g(x)的单调递减区间.
解(Ⅰ)f(x)=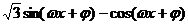
=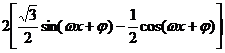
=2sin( -
- )
)
因为f(x)为偶函数,
所以对x∈R,f(-x)=f(x)恒成立,
因此sin(- -
- )=sin(
)=sin( -
- ).
).
即-sin cos(
cos(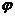 -
- )+cos
)+cos sin(
sin(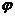 -
- )=sin
)=sin cos(
cos(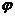 -
- )+cos
)+cos sin(
sin(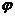 -
- ),
),
整理得 sin cos(
cos(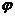 -
- )=0.因为
)=0.因为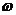 >0,且x∈R,所以cos(
>0,且x∈R,所以cos(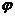 -
- )=0.
)=0.
又因为0<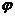 <π,故
<π,故 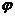 -
- =
= .所以f(x)=2sin(
.所以f(x)=2sin( +
+ )=2cos
)=2cos .
.
由题意得 ,所以
,所以
故 f(x)=2cos2x.
因为

(Ⅱ)将f(x)的图象向右平移个 个单位后,得到
个单位后,得到 的图象,再将所得图象横坐标伸长到原来的4倍,纵坐标不变,得到
的图象,再将所得图象横坐标伸长到原来的4倍,纵坐标不变,得到 的图象.
的图象.
所以
当 (k∈Z),
(k∈Z),
即4kπ+≤ ≤x≤4kπ+
≤x≤4kπ+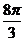 (k∈Z)时,g(x)单调递减.
(k∈Z)时,g(x)单调递减.
因此g(x)的单调递减区间为 (k∈Z)
(k∈Z)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com