
题目列表(包括答案和解析)
6.抛物线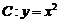 上两点
上两点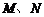 满足
满足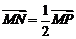 ,若
,若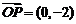 ,则
,则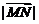 =
.
=
.
5.如图,过抛物线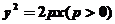 的焦点F的直线
的焦点F的直线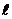 交抛物线于点A、B,
交抛物线于点A、B,
交其准线于点C,若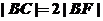 ,且
,且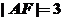 ,
,
则此抛物线的方程为 ______________
4.抛物线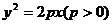 上三点横坐标成等差数列,那么这三点的焦半径成________数列.
上三点横坐标成等差数列,那么这三点的焦半径成________数列.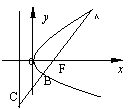
3.过抛物线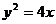 的焦点F作一直线交抛物线于P、Q两点,若线段PF与线段FQ的长分别为p,q则
的焦点F作一直线交抛物线于P、Q两点,若线段PF与线段FQ的长分别为p,q则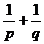 与1的大小关系是_________.
与1的大小关系是_________.
2.若双曲线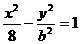 的一条准线与抛物线
的一条准线与抛物线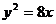 的准线重合,则双曲线的离心率为________
的准线重合,则双曲线的离心率为________
1.以抛物线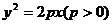 的焦半径| PF|为直径的圆与y轴的位置关系为________
的焦半径| PF|为直径的圆与y轴的位置关系为________
22.(本小题满分12分)已知数列{an}(n∈N*)是首项为a1公比为q的等比数列.
(1)求和a1C-a2C+a3C,a1C-a2C+a3C-a4C;
(2)由(1)的结果归纳概括出关于正整数n的一个结论,并加以证明.
解析:(1)a1C-a2C+a3C=a1-2a1q+a1q2=a1(1-q)2,a1C-a2C+a3C-a4C=a1-3a1q+3a1q2-a1q3=a1(1-q)3.
(2)归纳概括的结论为:
若数列{an}是首项为a1,公比为q的等比数列,则a1C-a2C+a3C-a4C+…+(-1)nan+1C=a1(1-q)n,n为正整数.
证明:a1C-a2C+a3C-a4C+…+(-1)nan+1C
=a1C-a1qC+a1q2C-a1q3C+…+(-1)na1qnC
=a1[C-qC+q2C-q3C+…+(-1)nqnC]
=a1(1-q)n.
21.(本小题满分12分)从5名男生、3名女生中选5人担任5门不同学科的课代表,分别求符合下列条件的方法数;
(1)女生甲担任语文课代表;
(2)男生乙必须是课代表,但不担任英语课代表;
(3)3名男课代表,2名女课代表,男生乙不任英语课代表.
分析:本题是先组合后排列问题,特殊情况可优先考虑.
解析:(1)女生甲担任语文课代表,再选四人分别担任其他四门学科课代表,方法数有CA=840种.
(2)先选出4人,有C种方法,连同乙在内,5人担任5门不同学科的课代表,乙不担任英语课代表,有A·A种方法,所以方法数为C·A·A=3360种.
(3)分两类,乙担任课代表,乙不担代课任表.
第一类:乙担任课代表,先选出2名男生2名女生,有CC种方法,连同乙在内,5人担任5门不同学科的课代表,乙不担任英语课代表,有AA种方法,方法数为CC·AA种;
第二类:乙不担任课代表,有CCA种方法.
根据分类计数原理,共有CCAA+CCA=3168种不同方法.
20.(本小题满分12分)已知在(-)n的展开式中,第6项为常数项.
(1)求n;
(2)求含x2的项的系数;
(3)求展开式中所有的有理项.
解析:(1)通项公式为
Tr+1=Cx(-3)rx-=C(-3)rx.
∵第6项为常数项,∴r=5时,有=0,
∴n=10.
(2)令=2,得r=(n-6)=2,
∴所求的系数为C(-3)2=405.
(3)根据通项公式,由题意,得
令=k(k∈Z),则
10-2r=3k,r=5-k.
∵r∈N,∴k应为偶数.
故k可取-2,0,2,即r可取2,5,8,所以第3项、第6项、第9项为有理项,它们分别为:
C(-3)2x2、C(-3)5、C(-3)8x-2.
19.(本小题满分12分)用0,1,2,3,4这五个数字,可以组成多少个满足下列条件的没有重复的五位数.
(1)被4整除;
(2)比21034大的偶数;
(3)左起第二、四位是奇数的偶数.
解析:(1)被4整除的数,其特征应是末两位数是4的倍数,可分两类:当末两位数是20,40,04时,其排列数为3A=18个,当末两位数是12,24,32时,其排列数为3·AA=12个,故满足条件的五位数共有
3A+3AA=30个.
(2)法一:可分五类,当末位数是0,而首位数是2时,
有AA+A=6个;
当末位数字是0,而首位数字是3或4时,
有AA=12个;
当末位数字是2,而首位数字是3或4时,有AA=12个;当末位数字是4,而首位数字是2时,有A+A=3个;当末位数字是4,而首位数字是3时,有A=6个.
故有(AA+A)+AA+AA+A+A+A=39个.
法二:不大于21034的偶数可分为三类:
万位数字为1的偶数,有AA=18个;
万位数字为2,而千位数字是0的偶数,有A个;
还有21034本身.
而由0,1,2,3,4组成的五位偶数有
A+AAA=60个.故满足条件的五位偶数共有60-AA-A-1=39个.
(3)法一:可分两类,0是末位数,有AA=4个,2或4是末位数,有AA=4个.故共有AA+AA=8个.
法二:第二、四位从奇数1,3中取,有A;首位从2,4中取,有A个;余下的排在剩下的两位,有A个,
故共有AAA=8个.
反思归纳:(1)数字排列问题,0不能排首位,特殊元素(特殊位置)应优先考虑;
(2)合理分类或分步,做到不重不漏;
(3)正难则反,注意间接法的应用.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com