
题目列表(包括答案和解析)
3.与两坐标轴都相切,且过点(2,1)的圆的方程为
[解析] 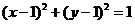 或
或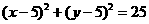
2. ( 广州六中2008-2009学年度高三期中考试) 若圆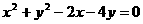 的圆心到直线
的圆心到直线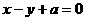 的距离为
的距离为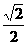 ,则a的值为(
)
,则a的值为(
)
A.-2或2 B. C.2或0 D.-2或0
C.2或0 D.-2或0
解析: C
圆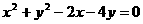 的圆心为(1,2),
的圆心为(1,2),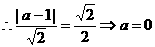 或2
或2
1.若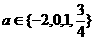 ,方程
,方程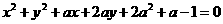 表示的圆的个数为( ).
表示的圆的个数为( ).
A、0个 B、1个 C、2个 D、3个
解析:B
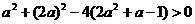 得
得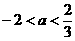 ,满足条件的
,满足条件的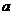 只有一个,方程
只有一个,方程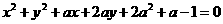 表示的圆的个数为1.
表示的圆的个数为1.
2.运用转化的思想处理圆的对称问题
问题2:圆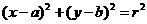 关于直线
关于直线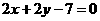 对称,则
对称,则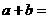
点拨:圆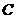 关于直线
关于直线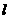 对称的实质是圆心
对称的实质是圆心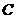 在直线
在直线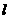 上,因此可将圆心坐标代入直线方程解决
上,因此可将圆心坐标代入直线方程解决
解析: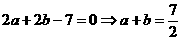
问题3:圆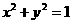 关于直线
关于直线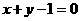 的对称圆的方程为
的对称圆的方程为
点拨:两圆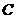 和
和 关于直线
关于直线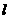 对称,可以转化为点对称问题(即圆心
对称,可以转化为点对称问题(即圆心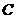 和
和 关于直线
关于直线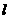 对称且半径相等),也可以用相关点法来处理,后一种方法更有推广价值
对称且半径相等),也可以用相关点法来处理,后一种方法更有推广价值
解析:方法1:原点关于直线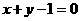 的对称点为(1,1),所以圆
的对称点为(1,1),所以圆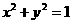 关于直线
关于直线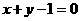 的对称圆的方程为
的对称圆的方程为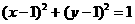
方法2:设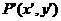 是圆
是圆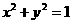 上一动点,它关于直线
上一动点,它关于直线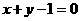 的对称点为
的对称点为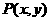 ,
,
则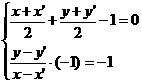
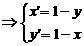
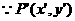 在圆
在圆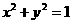 ,
, 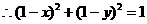
圆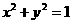 关于直线
关于直线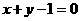 的对称圆的方程为
的对称圆的方程为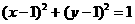
★热点考点题型探析★
考点1 圆的方程
题型1: 对圆的方程的认识
[例1 ]设方程x2+y2-2(m+3)x+2(1-4m2)y+16m4+9=0。
(1)当且仅当m在什么范围内,该方程表示一个圆。
(2)当m在以上范围内变化时,求半径最大的圆的方程。
(3)求圆心的轨迹方程
[解析](1)由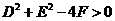 得:
得: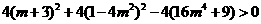 ,
,
化简得: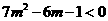 ,解得:
,解得: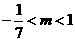 。
。
所以当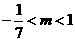 时,该方程表示一个圆。
时,该方程表示一个圆。
(2)r=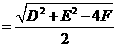 =
=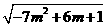 ,当
,当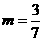 时,
时,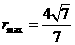
(3)设圆心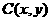 ,则
,则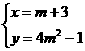 ,消去
,消去 得
得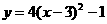

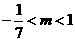
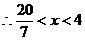
 所求的轨迹方程为
所求的轨迹方程为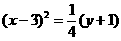
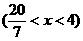
[名师指引](1)已知圆的一般方程,要能熟练求出圆心坐标、半径及掌握方程表示圆的条件;(2)第3问求圆心的轨迹方程,使用了参数法,即把x,y都表示成m的函数,消去参数可得到方程,用此法要注意变量x,y的范围
题型2: 求圆的方程
[例2](1)求经过点A(5,2),B(3,2),圆心在直线2x-y-3=0 上的圆的方程;
(2)求以O(0,0),A(2,0),B(0,4)为顶点的三角形OAB外接圆的方程。
[解题思路]根据条件,列方程组求参数
[解析](1)设圆心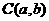 ,则有
,则有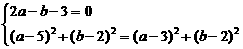
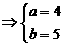
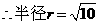 ,所求圆的方程为
,所求圆的方程为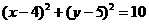
(2)采用一般式,设圆的方程为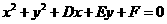 ,将三个已知点的坐标代入得
,将三个已知点的坐标代入得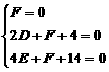 ,解得:
,解得: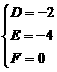
故所求圆的方程为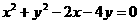
[名师指引](1)求圆的方程必须满足三个独立条件方可求解,选择方程的形式,合理列出方程组是关键,(2)当条件与圆心、半径有关时常选择标准方程,当条件是圆经过三个点时,常选用一般方程
[新题导练]
1.充分利用圆的几何性质解题
圆上的动点到已知直线(或点)的距离的最大值和最小值,转化为圆心到已知直线(或点)的距离来处理
问题1:已知圆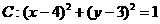 和点
和点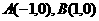 ,点P在圆上,求
,点P在圆上,求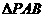 面积的最小值
面积的最小值
点拔:圆心(4,3)到直线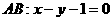 的距离为
的距离为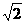 ,P到直线
,P到直线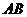 的距离的最小值为
的距离的最小值为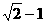 ,求
,求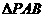 面积的最小值为
面积的最小值为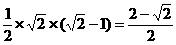
5、点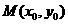 与圆
与圆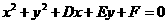 的位置关系:
的位置关系:
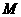 在圆内
在圆内
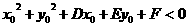
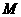 在圆上
在圆上
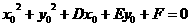
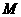 在圆外
在圆外
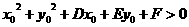
★重难点突破★
重点: 掌握确定圆的几何要素, 掌握圆的标准方程和圆的一般方程,
难点:根据已知条件,求圆的方程
重难点:围绕圆的几何性质进行合理转化,运用方程思想列出关于参数: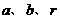 (或
(或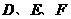 )得到方程组,进而求出圆的方程
)得到方程组,进而求出圆的方程
4. 若圆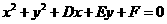 关于
关于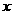 轴对称,则
轴对称,则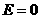 ;
;
若圆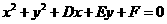 关于
关于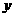 轴对称,则
轴对称,则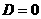 ;
;
若圆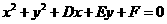 关于
关于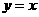 轴对称,则
轴对称,则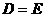 ;
;
3. 若圆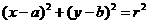 与
与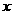 轴相切,则
轴相切,则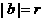 ;若圆
;若圆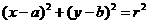 与
与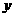 轴相切,则
轴相切,则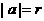
2.以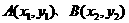 为直径端点的圆方程为
为直径端点的圆方程为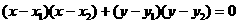
1. 圆的标准方程与一般方程
①圆的标准方程为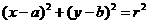 ,其中圆心为
,其中圆心为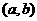 ,半径为r;
,半径为r;
②圆的一般方程为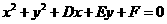 ,圆心坐标
,圆心坐标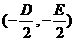 ,半径为
,半径为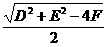 。方程表示圆的充要条件是
。方程表示圆的充要条件是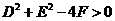
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com