1．已知m≠n，x＝m⁴－m³n，y＝n³m－n⁴，那么x、y的大小关系应是　　　　　　　 (　)

A．x＞y　　　　　　　　　 B．x＝y

C．x＜y　 　　　　　　　　　　　　　　　　 D．与m、n的取值有关

答案：A

解析：x－y＝m³(m－n)－n³(m－n)

＝(m－n)(m³－n³)

＝(m－n)²(m²+mn+n²)

＝(m－n)²[(m+)²+n²]＞0.则x＞y.

16．(2009·石家庄模拟)已知函数f(x)＝(a，b为常数)，且方程f(x)－x+12＝0有两个实根为x₁＝3，x₂＝4.

(1)求函数f(x)的解析式；

(2)设k＞1，解关于x的不等式f(x)＜.

解析：(1)将x₁＝3，x₂＝4分别代入方程－x+12＝0，

得，解得，

∴f(x)＝－(x≠2)．

(2)不等式即为＜，

可化为＜0，

即(x－2)(x－1)(x－k)＞0.

①当1＜k＜2时，解集为(1，k)∪(2，+∞)；

②当k＝2时，不等式为(x－2)²(x－1)＞0，解集为(1,2)∪(2，+∞)；

③当k＞2时，解集为(1,2)∪(k，+∞)．

15．已知不等式ax²－3x+6>4的解集为{x|x<1或x>b}，

(1)求a，b；

(2)解不等式>0(c为常数)．

解析：(1)由已知，1，b是方程ax²－3x+2＝0的两根，

∴⇒.

(2)原不等式为>0，等价于(x－c)(x－2)>0，

当c<2时，解集为{x|x<c或x>2}；

当c＝2时，解集为{x|x∈R且x≠2}；

当c>2时，解集为{x|x<2或x>c}．

14．已知f(x)＝x²+px+q，若f(x)<0的解集为(2,5)，试求不等式≤1的解集．

解析：由韦达定理得

解得p＝－7，q＝10

∴≤1即为≤1

≤0

即，

，

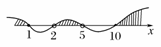
解得：x≤1或2<x<5或x≥10

∴不等式≤1的解集为(－∞，1]∪(2,5)∪[10，+∞)．

13．解下列不等式：

(1)(－3x+2)(4x+2)²(x－1)³(x－3)≤0；

(2)≤0.

解析：(1)∵不等式(－3x+2)(4x+2)²(x－1)³(x－3)≤0，

∴方程(－3x+2)(4x+2)²(x－1)³(x－3)＝0的根为，－，1,3，这些根把数轴分为5个区间(如图所示)．

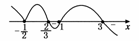
故原不等式的解集为{x|x＝－或≤x≤1或x≥3}．

(2)≤0⇔⇔⇔x＜－3或x≥0且x≠3.

∴原不等式的解集为{x|x＜－3或x≥0且x≠3}．

12．(2009·湖南名校一模)已知y＝f(x)是定义在R上的奇函数，当x＞0时，f(x)＝x－2，则不等式f(x)＜的解集是________．

答案：{x|x＜－或0≤x＜}

解析：∵f(x)在R上是奇函数，

∴f(x)＝则f(x)＜即

或或

所以f(x)＜的解集为{x|x＜－或0≤x＜}．

11．关于x的不等式ax²+bx+2＞0的解集为{x|－1＜x＜2}，则关于x的不等式bx²－ax－2＞0的解集为____．

答案：{x|x＜－2或x＞1}

解析：∵ax²+bx+2＞0的解集为{x|－1＜x＜2}，

∴⇒，

∴bx²－ax－2＞0即x²+x－2＞0.

解得x＞1或x＜－2.

10．不等式≤0的解集是________．

答案：[－3,2)

解析：≤0⇔⇒－3≤x＜2.

9．(2009·浙江台州一模)已知不等式x²－2x－3＜0的整数解构成等差数列{a_n}，则数列{a_n}的第四项为________．

答案：3或－1

解析：解x²－2x－3＜0得－1＜x＜3，

∴整数解是0,1,2.

∴d＝1或d＝－1，∴a₄＝3或a₄＝－1.

8．(2009·湖南十二校联考一，7)已知函数f(x)＝log_ax(a＞0且a≠1)满足f()＞f()，则f(1－)＞1的解是　　　　　　　　　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A．1＜x＜　 　　　　　　　　　　　 B．1＜x＜

C．0＜x＜　 　　　　　　　　　　　　　　 D．0＜x＜

答案：A

解析：函数f(x)＝log_ax(a＞0且a≠1)满足f()＞f()，则0＜a＜1，f(1－)＞1，即0＜1－＜a，不等式的解集是1＜x＜，故选A.