
题目列表(包括答案和解析)
11. 解:(1)如图1,连结DF.
因为点E为CD的中点,所以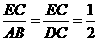 .
.
据题意可证△FEC∽△FBA,所以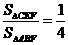 . (2分)
. (2分)
因为S△DEF=S△CEF,S△=S. (2分)
所以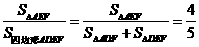 .
.
(2)如图2,连结DF.
与(1)同理可知,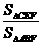 =
=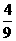 ,S△DEF=
,S△DEF=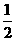 S△CEF,
S△CEF,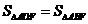 ,
,
所以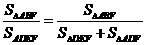 =
=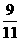 .
.
(3)当CE:ED=3:1时,=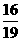 .
.
当CE:ED=n:1时, =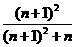 (=
(=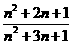 ).
).
(4)提问举例:①当点E运动到CE:ED=5:1时,△ABF与四边形ADEF的面积之比是多少?
②当点E运动到CE:ED=2:3时,△ABF与四边形ADEF的面积之比是多少?
③当点E运动到CE:ED=m:n(m,n是正整数)时,△ABF与四边形ADEF的面积之比是多少?
10. 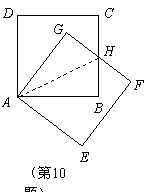 解:
解: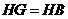 .
.
证法1:连结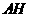 ,
,
 四边形
四边形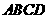 ,
,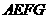 都是正方形.
都是正方形.

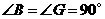 .
.
由题意知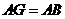 ,又
,又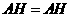 .
.
 ,
,
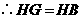 .
.
证法2:连结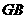 .
.
 四边形
四边形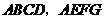 都是正方形,
都是正方形,
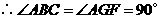 .
.
由题意知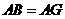 .
.
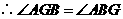 .
.
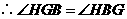 .
.
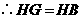 .
.
9. (1) 证明: 如图,∵ AD=CD,DE=DG,∠ADC=∠GDE=90o,
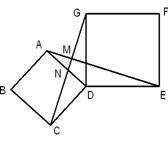 又 ∠CDG=90o
+∠ADG=∠ADE,
又 ∠CDG=90o
+∠ADG=∠ADE,
∴ △ADE≌△CDG. ∴ AE=CG.
(2)猜想: AE⊥CG.
证明: 如图,
设AE与CG交点为M,AD与CG交点为N.
∵ △ADE≌△CDG, ∴ ∠DAE=∠DCG.
又∵ ∠ANM=∠CND, ∴ △AMN∽△CDN.
∴ ∠AMN=∠ADC=90o.∴ AE⊥CG.
8.证明:(1)∵四边形ABCD是正方形.∴BC=DC,∠BCD=90°
在Rt△BCE和Rt△DCF中,BC=DC,CE=CF,∴Rt△BCE≌Rt△DCF
(2)∵CE=CF,∴∠CEF=∠CFE,∴∠CFE=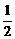 (180°-90°)=45°
(180°-90°)=45°
∵Rt△BCE≌Rt△DCF,∴∠CFD=∠BEC=60°
∴∠EFD=∠DFC-∠EFC=15°
6. 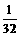 ;7.105;
;7.105;
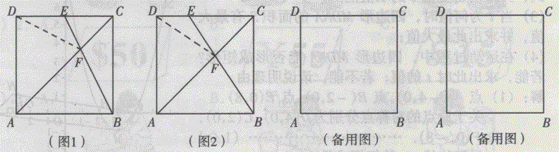
1.A;2.A; 3.∠A=90°或∠B=90°或∠C=90°或∠D=90°中的任一条件即可;4. D;5. 3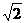 ;
;
11.如图,点E在正方形ABCD的边CD上运动,AC与BE交于点F.
(1)如图1,当点E运动到DC的中点时,求△ABF与四边形ADEF的面积之比;
(2)如图2,当点E运动到CE:ED=2:1时,求△ABF与四边形ADEF的面积之比.
(3)当点E运动到CE:ED=3:1时,写出△ABF与四边形ADEF的面积之比;当点E运动到CE:ED=n:1(n是正整数)时,猜想△ABF与四边形ADEF的面积之比(只写结果,不要求写出计算过程);
(4)请你利用上述图形,提出一个类似的问题(根据提出的问题给附加分,最多4分,计入总分,但总分不超过120分).
课时三答案:
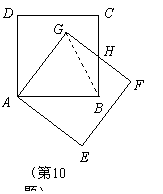
10.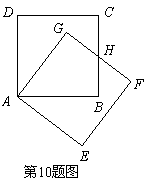 把正方形
把正方形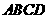 绕着点
绕着点 ,按顺时针方向旋转得到正方形
,按顺时针方向旋转得到正方形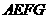 ,边
,边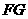 与
与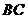 交于点
交于点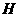 (如图).试问线段
(如图).试问线段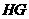 与线段
与线段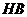 相等吗?
相等吗?
请先观察猜想,然后再证明你的猜想.
8. 已知如下图,正方形ABCD中,E是CD边上的一点,
F为BC延长线上一点,CE=CF.
(1)求证:△BEC≌△DFC;
(2)若∠BEC=60°,求∠EFD的度数.
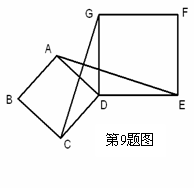 9如图所示,.四边形ABCD、DEFG都是正方形,连接AE、CG.
9如图所示,.四边形ABCD、DEFG都是正方形,连接AE、CG.
(1)求证:AE=CG;
(2)观察图形,猜想AE与CG之间的位置关系,
并证明你的猜想.
7.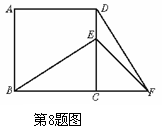 如图,四边形ABCD为正方形,△ADE为等边三角形,AC为正方形ABCD的对角线,则∠EAC=___度.
如图,四边形ABCD为正方形,△ADE为等边三角形,AC为正方形ABCD的对角线,则∠EAC=___度.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com