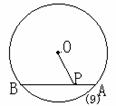
5、(97安徽)已知，如图(9)，AB是⊙O的弦，P是AB上一点，AB＝10cm，PA＝4cm，OP＝5cm，则⊙O的半径为＿＿＿＿

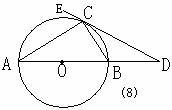
4、(96山西)如图(8)，AB是⊙O直径，点D在AB的延长线上，BD＝OB，若CD切⊙O于点C，则∠CAB的度数为＿＿＿＿＿，∠DCB＝＿＿＿，∠ECA的度数为＿＿＿＿＿

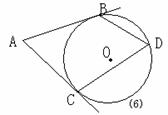
3、(99广东)如图(6)，AB、AC是⊙O的两条切线，切点分别是B、C，D是优弧BC

上的点，已知∠BAC＝50⁰，则∠BDC＝＿＿＿＿度。

2、(98上海)一个圆的弦切角等于40⁰，那么这个弦切角所夹

的弧所对的圆心角的度数是＿＿＿＿＿。

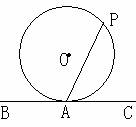
1、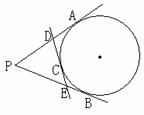(99辽宁)如图，PA分别切于⊙O于A、B，PA＝5，

在劣弧AB上取一点C，过C过作⊙O切线，分别交PA、PB

于D、E，则△PDE的周长等于＿＿＿＿。

3、遇到过圆外一点的两条切线时，常常引这点到圆心的连线，以便利用切线长定理及推论。

2、遇到切线时，一般要引过切点的半径，以便利用切线的性质定理，或者连结过切点的弦，以便利用弦切角定理。

1、遇到直径时，一般要引直径所对的圆周角，将直径这一条件转化为直角条件。

图形	定义	定理	推论
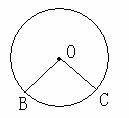	顶点在圆心上的角	圆心角的度数等于它所对弧的度数
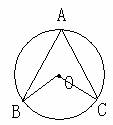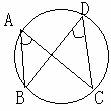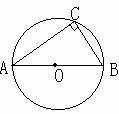	顶点在圆上，并且两边都与圆相交角	1、一条弧所对的圆周角等于它所对的圆心角的一半 2、圆周角定理：圆周角的度数等于它所对弧的度数的一半	1、同弧或等弧所对的圆周角相等。 2、同圆或等圆中，相等的圆周角所对的弧也相等。 3、半圆(或直径)所对的圆周角是直角：900的圆周角所对的弦是直径。
	顶点在圆上，并且一边和圆相交，另一边和圆相切的角叫弦切角	1、弦切角定理：弦切角等于它夹弧所对的圆周角。 2、弦切角的度数等于它所夹的弧的度数的一半	两个弦切角所夹的弧相等，两个弦切角也相等。

说明：在同圆或等圆中，圆心角相等弧相等弦相等弦心距相等，弧(劣)大　弦大弦心距小。

3、 如图8，△ABC中，AB=AC，经过A、B两点的⊙O与AC、BC分别交于M、N两点，过N点作⊙O的切线ND交AC于D。

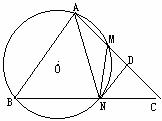求证：①MN=CN；②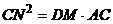；③若DN=2，AM=3，MN=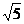求AB与BC的长。