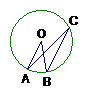
4．如图，A、B、C是⊙O上三点，若∠ACB＝20°，则∠AOB的度数为(　)

(A)10°　(B)20°　(C)30° (D)40°

3．足球比赛前，裁判通常要掷一枚硬币来决定比赛双方的场地与首发球者，其主要原因是(　)

(A)让比赛更富有情趣　　(B)让比赛更具有神秘色彩

(C)体现比赛的公平性 　　(D)不知道什么原因

2．如果函数y＝kx的图象经过点(－1，3)，那么k的值为(　)

(A)1　(B)－1　(C)3 (D)－3

1．有理数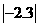在数轴上所表示的点的位置为(　)

(A)在原点的左侧　　　　　　　　(B)在原点的右侧　

(C)即可在原点的左侧，又可在在原点的右侧　　(D)不能确定

26、如图14，⊙O1和⊙2内切于点P。C是⊙O1上任一点(与点P不重合)。

实验操作：将直角三角板的直角顶点放在点C上，一条直角边经过点O1，另一直角边所在直线交⊙O2于点A、B，直线PA、PB分别交⊙O1于点E、F，连结CE(图15是实验操作备用图)

探究：⑴你发现弧CE、弧CF有什么关系？用你学过的知识证明你的发现；

⑵作发现线段CE、PE、BF有怎样的比例关系？证明你的发现。

附加题：如图16，若将上述问题的⊙O1和⊙O2由内切认为外切，其它条件不变，请你探究线段CE、PE、BF有怎样的比例关系，并说明。

24、如图11，⊙O的直径DF与弦AB交于点E，C为⊙O外一点，

CB⊥AB，G是直线CD上一点，∠ADG=∠ABD。

求证：AD·CE=DE·DF

说明：⑴如果你经历反复探索，没有找到解决问题的方法，请你把探索过程中的某种思路过程写出来(要求至少写3步)；

⑵在你经历说明⑴的过程之后，可以从下列①、②、③中

选取一个补充或更换已知条件，完成你的证明。

注意：选取①完成证明得8分；选取②完成证明得6分；选取③完成证明得4分。

①∠CDB=∠CEB；

②AD∥EC；

③∠DEC=∠ADF，且∠CDE=90°。

23、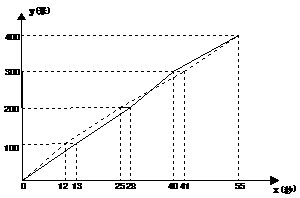4×100米拉力赛是学校运动会最精彩的项目之一。图10中的实线和虚线分别是初三·一班和初三·班代表队在比赛时运动员所跑的路程y(米)与所用时间x(秒)的函数图象(假设每名运动员跑步速度不变，交接棒时间忽略不计)。

问题：

⑴初三·二班跑得最快的是第______接力棒的运动员；

⑵发令后经过多长时间两班运动员第一次并列？

22、如图9－⑴、9－⑵、…、9－(m)是边长均大于2的三角形、四边形、…、凸n边形。分别以它们的各顶点为圆心，以1为半径画弧与两邻边相交，得到3条弧、4条弧……、n条弧。

⑴图9－⑴中3条弧的弧长的和为_________________，

图9－⑵中4条弧的弧长的和为__________________；

⑵求9－(m)中n条弧的弧长的和(用n表示)。

21、如图8，抛物线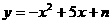经过点A(1，0)，与y轴交于点B。

⑴求抛物线的解析式；

⑵P是y轴正半轴上一点，且△PAB是以AB为腰的等腰三角形，试求P点坐标。