
题目列表(包括答案和解析)
14.解:(1)投资封闭式基金的收益与投资额的函数关系为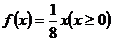 ;
;
投资开放式基金的收益与投资额的函数关系式为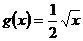
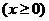 .
.
(2)设投资封闭式基金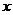 万元,则投资开放式基金为
万元,则投资开放式基金为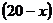 万元,共收益
万元,共收益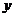 万元,
万元,
∴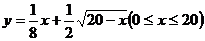 .令
.令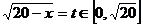 ,∴
,∴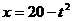 ,
,
∴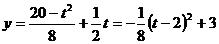 ,∴
,∴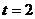 时,
时,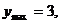 此时,
此时,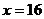 .
.
答:投资封闭式基金16万元,开放式基金4万元时,其收益最大,最大为3万元.
13.解:(Ⅰ)依题意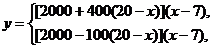
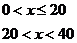
∴ 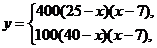
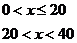 .此函数的定义域为
.此函数的定义域为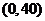 .
.
(Ⅱ)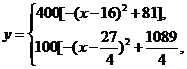
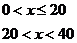 ,当
,当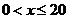 ,则当
,则当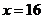 时,
时,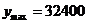 (元);当
(元);当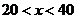 ,则当
,则当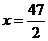 时,
时,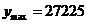 (元);
(元);
综上可得:当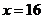 时,该特许专营店获得的利润最大为32400元.
时,该特许专营店获得的利润最大为32400元.
12.解:(1)当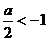 即
即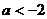 时,
时,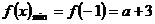 ,
,
此时,令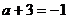 ,解得
,解得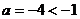 ,满足题意.
,满足题意.
(2)当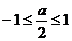 即
即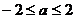 时,
时,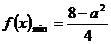 ,
,
此时,令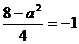 ,解得
,解得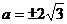 ,不满足题意 .
,不满足题意 .
(3)当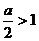 即
即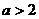 时
时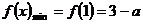 ,此时令
,此时令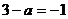 得
得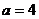 ,满足题意.
,满足题意.
综上,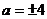 为所求的值.
为所求的值.
11.(1)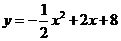 ,
,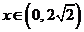 ;(2)
;(2)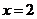 时,
时,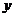 取到最大值10.
取到最大值10.
6. 7.2 8.①④ 9.(1,8.2) 10.①②④⑤
7.2 8.①④ 9.(1,8.2) 10.①②④⑤
1.3 2.1和3 3.0 4.720 5.4
14.(本题满分14分)王先生用购买基金的方法进行理财投资,根据长期收益效率市场预测,投资封闭式基金的收益与投资额成正比,投资开放式基金的收益与投资额的算术平方根成正比. 已知投资1万元时两类产品的收益分别为0.125万元和0.5万元(如图) .
(1) 分别写出投资两种基金的收益与投资额的函数关系;
(2) 王先生现有20万元资金,全部用于购买基金,问:怎样分配资金能使投资获得最大收益,其最大收益为多少?


函数与方程、函数模型及应用答案
13.(本题满分12分)某特许专营店销售北京奥运会纪念章,每枚进价为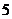 元,每销售一枚这种纪念章还需向北京奥组委交特许经营管理费
元,每销售一枚这种纪念章还需向北京奥组委交特许经营管理费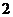 元,预计这种纪念章以每枚
元,预计这种纪念章以每枚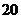 元的价格销售时该店一年可销售
元的价格销售时该店一年可销售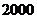 枚,经过市场调研发现每枚纪念章的销售价格在每枚
枚,经过市场调研发现每枚纪念章的销售价格在每枚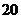 元的基础上每减少一元则增加销售
元的基础上每减少一元则增加销售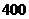 枚,每增加一元则减少销售
枚,每增加一元则减少销售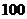 枚,现设每枚纪念章的销售价格定为
枚,现设每枚纪念章的销售价格定为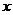 元.
元.
(1)写出该特许专营店一年内销售这种纪念章所获得的利润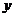 (元)与每枚纪念章的销售价格
(元)与每枚纪念章的销售价格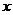 的函数关系式(写出这个函数的定义域);
的函数关系式(写出这个函数的定义域);
(2)当每枚纪念章销售价格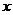 为多少时,该特许专营店一年内利润
为多少时,该特许专营店一年内利润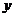 (元)最大,并求出这个最大值.
(元)最大,并求出这个最大值.
12.(本题满分12分)函数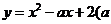 为常数)
为常数)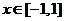 时的最小值为-1,求
时的最小值为-1,求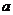 的值.
的值.
11.(本题满分12分)如右图半径为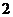 的圆内接等腰梯形
的圆内接等腰梯形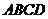 ,它的下底
,它的下底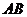 是⊙
是⊙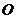 的直径,上底
的直径,上底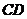 的端点在圆周上.
的端点在圆周上.
(1)写出这个梯形周长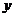 和腰长
和腰长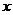 间的函数式,并求出它的定义域;
间的函数式,并求出它的定义域;
(2)求出周长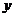 的最大值及相应
的最大值及相应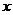 的值.
的值.

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com