
题目列表(包括答案和解析)
7、已知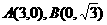 ,
, 为坐标原点,点
为坐标原点,点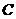 在第一象限内,且
在第一象限内,且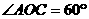 ,设
,设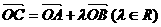 ,则
,则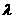 等于
等于
A. 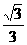 B.
B.
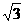 C.
C.
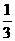 D.
D. 
6、若角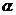 是第二象限角,且
是第二象限角,且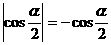 ,则角
,则角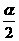 是
是
A.第一象限角 B.第二象限角 C.第三象限角 D.第四象限角
5、在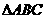 中,若
中,若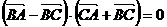 ,则
,则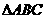 一定是
一定是
A.直角三角形 B.等腰三角形 C.等腰直角三角形 D.等边三角形
4、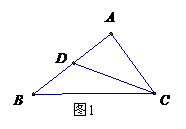 如图1所示,在
如图1所示,在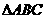 中,点
中,点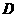 是边
是边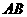 的中点,则向量
的中点,则向量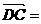
A. 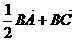 B.
B.
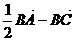
C. 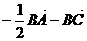 D.
D. 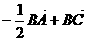
3、点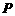 从
从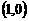 出发,沿单位圆逆时针方向运动
出发,沿单位圆逆时针方向运动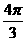 弧长到达
弧长到达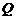 点,则
点,则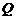 点的坐标为
点的坐标为
A.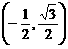 B.
B.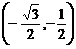 C.
C.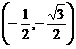
 D.
D.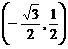
2、函数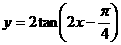 的定义域是
的定义域是
A.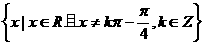 B.
B.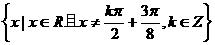
C.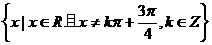 D.
D.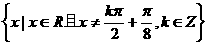
1、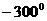 化为弧度是
化为弧度是
A. 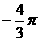 B.
B. 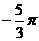 C.
C. 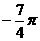 D.
D. 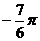
22.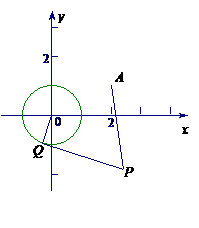 已知圆O:
已知圆O: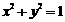 和定点A(2,1),由圆O外一点
和定点A(2,1),由圆O外一点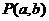 向圆O引切线PQ,切点为Q,且满足
向圆O引切线PQ,切点为Q,且满足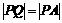 .
.
(1) 求实数a、b间满足的等量关系;
(2) 求线段PQ长的最小值;
(3) 若以P为圆心所作的圆P与圆O有公共点,试求半径取最小值时圆P的方程.
解:(1)连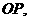
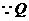 为切点,
为切点,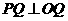 ,由勾股定理有
,由勾股定理有
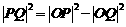 .又由已知
.又由已知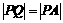 ,k+s-5#u
,k+s-5#u 
故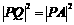 .
.
即: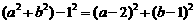 .
.
化简得实数a、b间满足的等量关系为: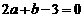 .
.
(2)由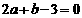 ,得
,得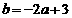 .
.
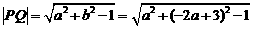
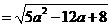 =
=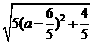 .
.
故当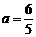 时,
时,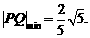 即线段PQ长的最小值为
即线段PQ长的最小值为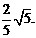 k+s-5#u
k+s-5#u 
解法2:由(1)知,点P在直线l:2x + y-3 = 0 上.
∴ | PQ |min = | PA |min ,即求点A 到直线 l 的距离.
∴ | PQ |min = = .
(3)设圆P 的半径为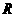 ,
, 圆P与圆O有公共点,圆O的半径为1,
圆P与圆O有公共点,圆O的半径为1,
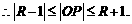 即
即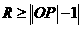 且
且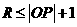 .
.
而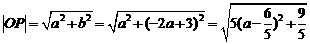 ,k+s-5#u
,k+s-5#u 
故当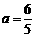 时,
时,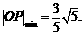 此时,
此时, 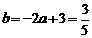 ,
,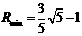 .
.
得半径取最小值时圆P的方程为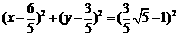 .
.
解法2: 圆P与圆O有公共点,圆P半径最小时为与圆O外切(取小者)的情形,而这些半径的最小值为圆心O到直线l的距离减去1,圆心P为过原点与l垂直的直线l’ 与l的交点P0.
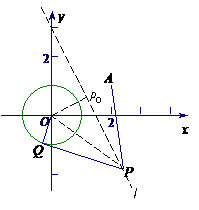 r = -1 = -1. k+s-5#u
r = -1 = -1. k+s-5#u 
又 l’:x-2y = 0,
解方程组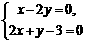 ,得
,得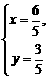 .即P0( ,).
.即P0( ,).
∴ 所求圆方程为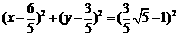 .
.
21.已知函数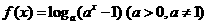 .
.
(1)求函数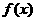 的定义域;
的定义域;
(2)讨论函数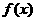 的单调性.
的单调性.
解:(1)函数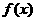 有意义,则
有意义,则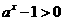 ……1分k+s-5#u
……1分k+s-5#u 
当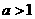 时,由
时,由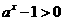 解得
解得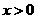 ;
;
当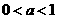 时,由
时,由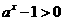 解得
解得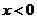 .
.
所以当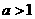 时,函数的定义域为
时,函数的定义域为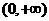 ;
……3分
;
……3分
当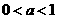 时,函数的定义域为
时,函数的定义域为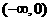 . ……5分
. ……5分
(2)当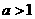 时,任取
时,任取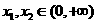 ,且
,且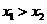 ,则
,则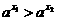
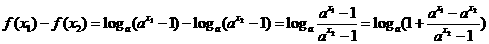
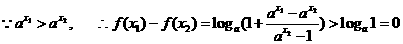 ,k+s-5#u
,k+s-5#u 
即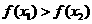
由函数单调性定义知:当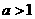 时,
时,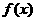 在
在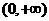 上是单调递增的. ……9分
上是单调递增的. ……9分
当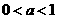 时,任取
时,任取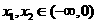 ,且
,且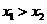 ,则
,则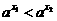
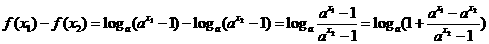
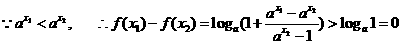 k+s-5#u
k+s-5#u 
即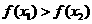
由函数单调性定义知:当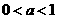 时,
时,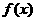 在
在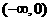 上是单调递增的. ……12分
上是单调递增的. ……12分
20.为了绿化城市,准备在如图所示的区域内修建一个矩形PQRC的草坪,
且PQ∥BC, RQ⊥BC,另外△AEF的内部有一文物保护区.AB=100m,BC=80m,AE=30m,AF=20m.
(3) 求直线EF的方程(4 分 ).
(4) 应如何设计才能使草坪的占地面积最大?(8 分 ).
解:(1)如图,在线段EF上任取一点Q,分别向BC,CD作垂线.k+s-5#u 
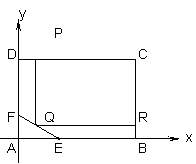 由题意,直线EF的方程为:+=1
由题意,直线EF的方程为:+=1
(2)设Q(x,20-x),则长方形的面积
S=(100-x)[80-(20-x)] (0≤x≤30)
化简,得 S= -x2+x+6000 (0≤x≤30)
配方,易得x=5,y=时,S最大,其最大值为6017m2
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com