
题目列表(包括答案和解析)
1 若函数
若函数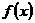 既是幂函数又是反比例函数,则这个函数是
既是幂函数又是反比例函数,则这个函数是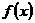 =
=

2 幂函数
幂函数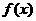 的图象过点
的图象过点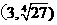 ,则
,则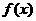 的解析式是_____________
的解析式是_____________
3 用“二分法”求方程
用“二分法”求方程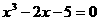 在区间
在区间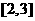 内的实根,取区间中点为
内的实根,取区间中点为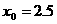 ,那么下一个有根的区间是
,那么下一个有根的区间是

4 函数
函数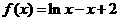 的零点个数为
的零点个数为

5 设函数
设函数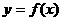 的图象在
的图象在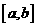 上连续,若满足
,方程
上连续,若满足
,方程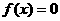
在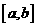 上有实根
上有实根
1 若
若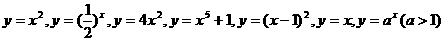
上述函数是幂函数的个数是( )
A
 个 B
个 B
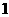 个 C
个 C
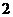 个 D
个 D
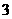 个
个
2 已知
已知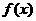 唯一的零点在区间
唯一的零点在区间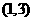 、
、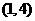 、
、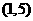 内,那么下面命题错误的( )
内,那么下面命题错误的( )
A 函数
函数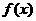 在
在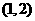 或
或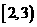 内有零点
内有零点
B 函数
函数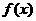 在
在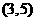 内无零点
内无零点
C 函数
函数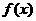 在
在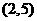 内有零点
内有零点
D 函数
函数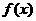 在
在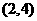 内不一定有零点
内不一定有零点
3 若
若 ,
,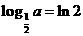 ,则
,则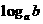 与
与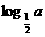 的关系是( )
的关系是( )
A
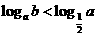 B
B
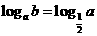
C
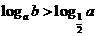 D
D
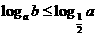
4 求函数
求函数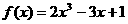 零点的个数为 ( )
零点的个数为 ( )
A
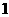 B
B
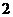 C
C
 D
D
5 已知函数
已知函数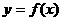 有反函数,则方程
有反函数,则方程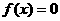 ( )
( )
A 有且仅有一个根 B
有且仅有一个根 B 至多有一个根
至多有一个根
C 至少有一个根 D
至少有一个根 D 以上结论都不对
以上结论都不对
6 如果二次函数
如果二次函数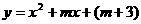 有两个不同的零点,则
有两个不同的零点,则 的取值范围是( )
的取值范围是( )
A
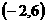 B
B
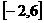 C
C
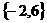 D
D
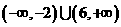
7 某林场计划第一年造林
某林场计划第一年造林 亩,以后每年比前一年多造林
亩,以后每年比前一年多造林 ,则第四年造林( )
,则第四年造林( )
A
 亩 B
亩 B
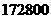 亩 C
亩 C
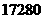 亩 D
亩 D
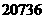 亩
亩
1 利用函数图象判断下列方程有没有实数根,有几个实数根:
利用函数图象判断下列方程有没有实数根,有几个实数根:
①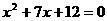 ;②
;②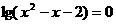 ;
;
③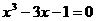 ; ④
; ④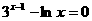

2 借助计算器,用二分法求出
借助计算器,用二分法求出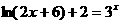 在区间
在区间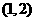 内的近似解(精确到
内的近似解(精确到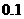 )
)
3 证明函数
证明函数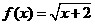 在
在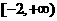 上是增函数
上是增函数
4 某电器公司生产
某电器公司生产 种型号的家庭电脑,
种型号的家庭电脑,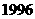 年平均每台电脑的成本
年平均每台电脑的成本 元,并以纯利润
元,并以纯利润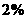 标定出厂价
标定出厂价
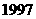 年开始,公司更新设备、加强管理,逐步推行股份制,从而使生产成本逐年降低
年开始,公司更新设备、加强管理,逐步推行股份制,从而使生产成本逐年降低
 年平均每台电脑出厂价仅是
年平均每台电脑出厂价仅是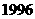 年出厂价的
年出厂价的 ,但却实现了纯利润
,但却实现了纯利润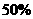 的高效率
的高效率
① 年的每台电脑成本;
年的每台电脑成本;
②以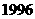 年的生产成本为基数,用“二分法”求
年的生产成本为基数,用“二分法”求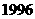 年至
年至 年生产成本平均每年降
年生产成本平均每年降
低的百分率(精确到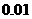 )
)
(数学1必修)第三章 函数的应用 [综合训练B组]
1
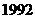 年底世界人口达到
年底世界人口达到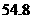 亿,若人口的年平均增长率为
亿,若人口的年平均增长率为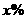 ,
, 年底世界人口
年底世界人口
为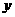 亿,那么
亿,那么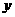 与
与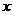 的函数关系式为
的函数关系式为

2
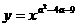 是偶函数,且在
是偶函数,且在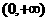 是减函数,则整数
是减函数,则整数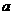 的值是
的值是

3 函数
函数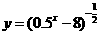 的定义域是
的定义域是

4 已知函数
已知函数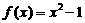 ,则函数
,则函数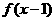 的零点是__________
的零点是__________
5 函数
函数 是幂函数,且在
是幂函数,且在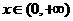 上是减函数,则实数
上是减函数,则实数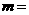 ______
______
1 若函数
若函数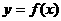 在区间
在区间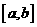 上的图象为连续不断的一条曲线,
上的图象为连续不断的一条曲线,
则下列说法正确的是( )
A 若
若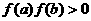 ,不存在实数
,不存在实数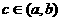 使得
使得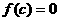 ;
;
B 若
若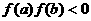 ,存在且只存在一个实数
,存在且只存在一个实数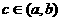 使得
使得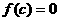 ;
;
C 若
若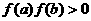 ,有可能存在实数
,有可能存在实数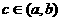 使得
使得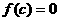 ;
;
D 若
若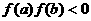 ,有可能不存在实数
,有可能不存在实数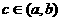 使得
使得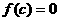 ;
;
2 方程
方程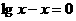 根的个数为( )
根的个数为( )
A 无穷多 B
无穷多 B
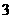 C
C
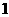 D
D

3 若
若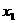 是方程
是方程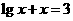 的解,
的解,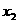 是
是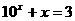 的解,
的解,
则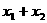 的值为( )
的值为( )
A
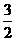 B
B
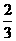 C
C
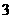 D
D
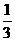
4 函数
函数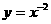 在区间
在区间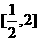 上的最大值是( )
上的最大值是( )
A
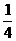 B
B
 C
C
 D
D
5 设
设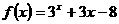 ,用二分法求方程
,用二分法求方程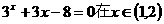
内近似解的过程中得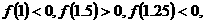
则方程的根落在区间( )
A
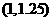 B
B
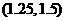
C
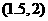 D
D 不能确定
不能确定
6 直线
直线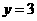 与函数
与函数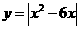 的图象的交点个数为( )
的图象的交点个数为( )
A
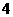 个 B
个 B
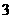 个 C
个 C
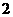 个 D
个 D
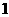 个
个
7 若方程
若方程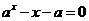 有两个实数解,则
有两个实数解,则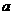 的取值范围是( )
的取值范围是( )
A
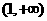 B
B
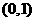
C
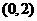 D
D
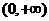
1 已知
已知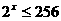 且
且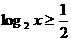 ,求函数
,求函数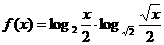 的最大值和最小值
的最大值和最小值
2 建造一个容积为
建造一个容积为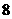 立方米,深为
立方米,深为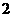 米的无盖长方体蓄水池,池壁的造价为每平方米
米的无盖长方体蓄水池,池壁的造价为每平方米 元,池底的造价为每平方米
元,池底的造价为每平方米 元,把总造价
元,把总造价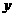 (元)表示为底面一边长
(元)表示为底面一边长 (米)的函数
(米)的函数
3 已知
已知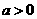 且
且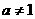 ,求使方程
,求使方程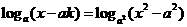 有解时的
有解时的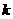 的取值范围
的取值范围
(数学1必修)第三章 函数的应用 [提高训练C组]
1 函数
函数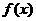 对一切实数
对一切实数 都满足
都满足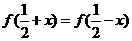 ,并且方程
,并且方程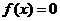 有三个实根,则这三个实根的和为
有三个实根,则这三个实根的和为
2 若函数
若函数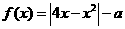 的零点个数为
的零点个数为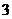 ,则
,则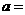 ______
______
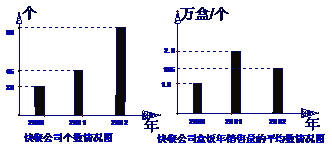
3 一个高中研究性学习小组对本地区
一个高中研究性学习小组对本地区 年至
年至 年快餐公司发展情况进行了调查,制成了该地区快餐公司个数情况的条形图和快餐公司盒饭年销售量的平均数情况条形图(如图),根据图中提供的信息可以得出这三年中该地区每年平均销售盒饭 万盒
年快餐公司发展情况进行了调查,制成了该地区快餐公司个数情况的条形图和快餐公司盒饭年销售量的平均数情况条形图(如图),根据图中提供的信息可以得出这三年中该地区每年平均销售盒饭 万盒
4 函数
函数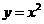 与函数
与函数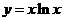 在区间
在区间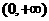 上增长较快的一个是
上增长较快的一个是

5 若
若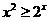 ,则
,则 的取值范围是____________
的取值范围是____________
1 函数
函数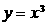 ( )
( )
A 是奇函数,且在
是奇函数,且在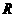 上是单调增函数
上是单调增函数
B 是奇函数,且在
是奇函数,且在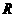 上是单调减函数
上是单调减函数
C 是偶函数,且在
是偶函数,且在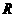 上是单调增函数
上是单调增函数
D 是偶函数,且在
是偶函数,且在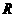 上是单调减函数
上是单调减函数
2 已知
已知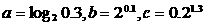 ,则
,则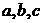 的大小关系是( )
的大小关系是( )
A
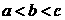 B
B
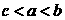
C
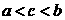 D
D
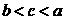
3 函数
函数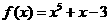 的实数解落在的区间是( )
的实数解落在的区间是( )
A
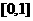 B
B
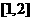 C
C
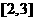 D
D
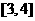
4 在
在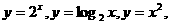 这三个函数中,当
这三个函数中,当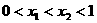 时,
时,
使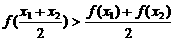 恒成立的函数的个数是( )
恒成立的函数的个数是( )
A
 个 B
个 B
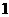 个 C
个 C
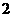 个 D
个 D
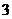 个
个
5 若函数
若函数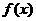 唯一的一个零点同时在区间
唯一的一个零点同时在区间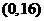 、
、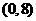 、
、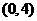 、
、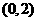 内,
内,
那么下列命题中正确的是( )
A 函数
函数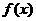 在区间
在区间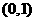 内有零点
内有零点
B 函数
函数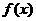 在区间
在区间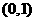 或
或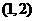 内有零点
内有零点
C 函数
函数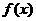 在区间
在区间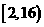 内无零点
内无零点
D 函数
函数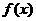 在区间
在区间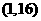 内无零点
内无零点
6 求
求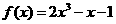 零点的个数为 ( )
零点的个数为 ( )
A
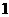 B
B
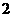 C
C
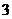 D
D
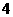
7 若方程
若方程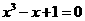 在区间
在区间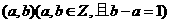 上有一根,则
上有一根,则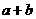 的值为( )
的值为( )
A
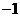 B
B
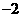 C
C
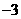 D
D
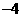
21.已知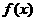 =2+
=2+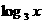
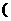 1≤
1≤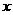 ≤9
≤9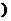 ,求函数
,求函数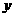 =
=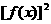 +
+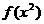 的最大值和最小值及相应的
的最大值和最小值及相应的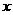 的值.
的值.
解: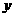 =
=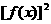 +
+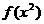 =
=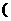 2+
2+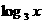
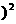 +2+
+2+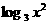
=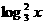 +6
+6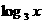 +6=
+6=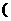
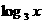 +3
+3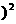 -3,
-3,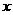 ∈
∈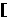 1,3
1,3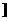 ,
,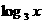 ∈
∈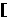 0,1
0,1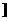 ,
,
∴当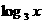 =0即
=0即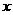 =1时,
=1时,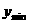 =6;
=6;
当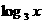 =1即
=1即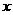 =3时,
=3时,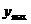 =13.
=13.
20.解下列关于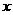 的方程:
的方程:
(1)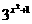 =81×
=81×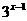 (2)
(2)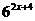 =
=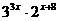
解:∵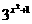 =
=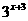 ,
解:
,
解: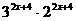 =
=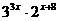 ,
,
∴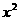 +1=
+1=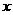 +3,
+3,
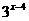 =
=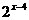 ,
,
得: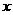 =-1或
=-1或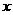 =2.
得:
=2.
得: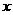 =4.
=4.
(3)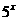 -
-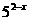 +24=0
(4)3×
+24=0
(4)3×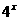 +2×
+2×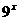 =5×
=5×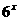
解: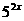 +24×
+24×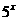 -25=0,
解:3×
-25=0,
解:3×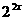 -5×
-5×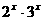 +2×
+2×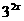 =0,
=0,
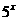 =1,
=1,
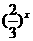 =
=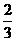 或
或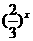 =1,
=1,
得: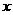 =0.
得:
=0.
得: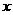 =1或
=1或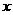 =0.
=0.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com