
题目列表(包括答案和解析)
12、解:(1)令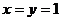 ,则
,则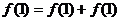 ,∴
,∴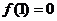 (2分)
(2分)  令
令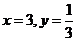 , 则
, 则 , ∴
, ∴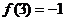 (4分)
(4分)
∴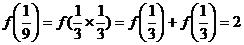 (6分)
(6分)
∴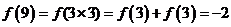 (8分)
(8分)
(2)∵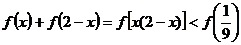 ,
,
又由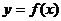 是定义在R+上的减函数,得:
是定义在R+上的减函数,得: 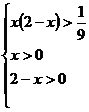 (12分)
(12分) 

解之得: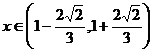 。 (14分)
。 (14分)
11、解:(1)因为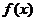 是开口向上的二次函数,且对称轴为
是开口向上的二次函数,且对称轴为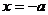 ,为了使
,为了使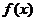 在
在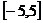 上是单调函数,故
上是单调函数,故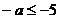 或
或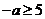 ,即
,即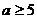 或
或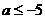 .
(5分)
.
(5分)
(2)当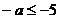 ,即
,即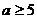 时,
时,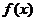 在
在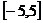 上是增函数,
上是增函数,
所以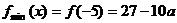 (7分)
(7分)
当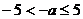 ,即
,即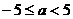 时,
时,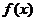 在
在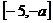 上是减函数,在
上是减函数,在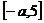 上是增函数,所以
上是增函数,所以 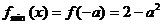 (9分)
(9分)
当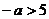 ,即
,即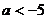 时,
时,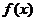 在
在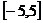 上是减函数,所以
上是减函数,所以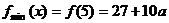
综上可得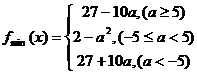 (12分)
(12分)
10.解:由S=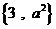 且S∩T=
且S∩T=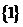 得
得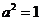 (2分)
(2分)
则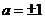 ,而S=
,而S=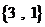 (4分)
(4分)
当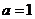 时,
时,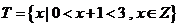
即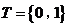 满足S∩T=
满足S∩T=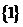 (6分)
(6分)
当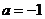 时,
时,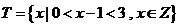
即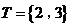 不满足S∩T=
不满足S∩T=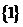 (9分)
(9分) 

所以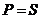 ∪
∪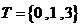 那么
那么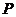 的子集有:
的子集有:
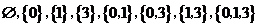 (12分)
(12分)
8. (1) ∵ A∩B=Φ
(2) ∵A∪B=B A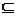 B
B
∴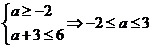 (6分) ∴
(6分) ∴
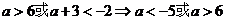 (12分)
(12分)
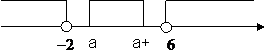

9证明:∵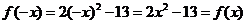 ∴函数
∴函数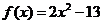 是偶函数 (5分)
是偶函数 (5分)
设任意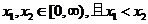 , 则
, 则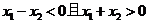
∴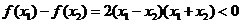 即
即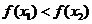


∴函数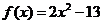 在
在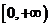 上是增加的。 (12分)
上是增加的。 (12分)
7、(1)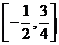 (2)
(2)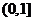
6.解:令x=y=1则f(1x1)=f(1)+ f(1),故f(1)=0
(2)由题意知x>0,且2/3-x>0,
而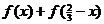 =f[x(2/3-x)]≤f(1/3)+ f(1/3)= f(1/9)
=f[x(2/3-x)]≤f(1/3)+ f(1/3)= f(1/9) 

因为函数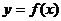 是定义在
是定义在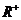 上的减函数,
上的减函数,
故x(2/3-x)≥1/9,故x=1/3∈(0,2/3)
5. 解:显然当P在AB上时,PA=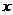 ;
;
当P在BC上时,PA=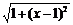 ;
;
当P在CD上时, PA=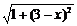 ;
;
当P在DA上时,PA=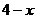 ,
,
再写成分段函数的形式. 

4.解(1)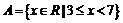 ,
,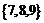 (2)
(2)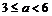
3、解:
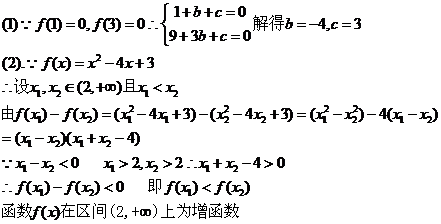


2. 解:①.因为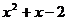 在分母上
在分母上
∴ 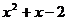 ≠0
≠0
∴ x≠1或x≠-2
该函数的定义域为:{x︱x≠1或x≠-2}
②.令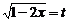 ,
,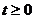 ,
,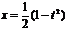 ,
,
原式等于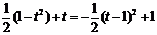 ,
,
故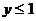 。
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com