
题目列表(包括答案和解析)
5.正六棱台的上、下底面的边长分别为a、b(a<b),侧面和底面所成的二面角为60°,则它的侧面积是( )
A.3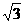 (b2-a2) B.2
(b2-a2) B.2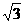 (b2-a2)
(b2-a2)
C.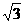 (b2-a2) D.
(b2-a2) D.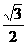 (b2-a2)
(b2-a2)
4.中心角为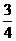 π,面积为B的扇形围成一个圆锥,若圆锥的全面积为A,则A∶B等于( )
π,面积为B的扇形围成一个圆锥,若圆锥的全面积为A,则A∶B等于( )
A.11∶8 B.3∶8 C.8∶3 D.13∶8
3.边长为5cm的正方形EFGH是圆柱的轴截面,则从正点沿圆柱的侧面到相对顶点G的最短距离是( )
A.10cm
B.5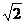 cm
cm
C.5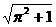 cm D.
cm D.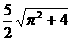 cm
cm
2.三棱柱ABC-A1B1C1中,AB=AC,且侧面A1ABB1与侧面A1ACCl的面积相等,则∠BB1C1等于( )
A.45° B.60° C.90° D.120°
1.正四棱柱的对角线长是9cm,全面积是144cm2,则满足这些条件的正四棱柱的个数是( )
A.0个 B.1个 C.2个 D.无数个
4.3空间直角坐标系
第1题. 在空间直角坐标系中,点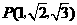 ,过点
,过点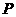 作平面
作平面 的垂线
的垂线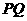 ,则
,则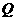 的坐标为( )
的坐标为( )
A.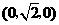 B.
B.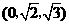 C.
C.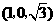 D.
D.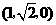
答案:D.
第2题. 已知点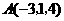 ,则点
,则点 关于原点的对称点的坐标为( )
关于原点的对称点的坐标为( )
A.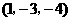 B.
B.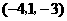
C.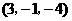 D.
D.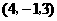
答案:C.
第3题. 在 平面内的直线
平面内的直线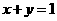 上确定一点
上确定一点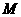 ,使
,使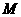 到点
到点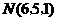 的距离最小.
的距离最小.
答案:解:由已知,可设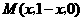 ,
,
则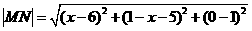
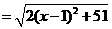 .
.
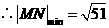 .
.
第4题. 求到两定点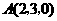 ,
,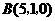 距离相等的点的坐标
距离相等的点的坐标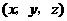 满足的条件.
满足的条件.
答案:解:设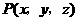 为满足条件的任一点,则由题意,
为满足条件的任一点,则由题意,
得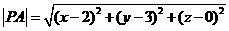 ,
,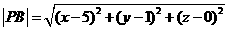 .
.
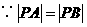 ,
,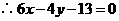 即为所求点所满足的条件.
即为所求点所满足的条件.
第5题. 在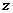 轴上与点
轴上与点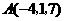 和点
和点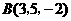 等距离的点
等距离的点 的坐标为 .
的坐标为 .
答案: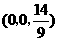
第6题. 已知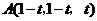 ,
,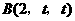 ,则
,则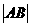 的最小值为( )
的最小值为( )
A.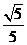 B.
B.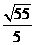 C.
C.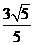 D.
D.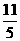
答案:C.
第7题. 已知三角形的三个顶点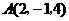 ,
,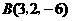 ,
,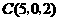 .则
.则
(1)过 点的中线长为 ;
点的中线长为 ;
(2)过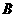 点的中线长为 ;
点的中线长为 ;
(3)过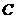 点的中线长为 .
点的中线长为 .
答案: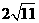 ;
;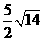 ;
;
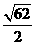
第8题. 已知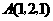 ,
,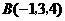 ,
,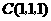 ,
,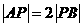 ,则
,则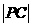 长为 .
长为 .
答案: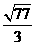 .
.
第9题. 给定空间直角坐标系,在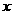 轴上找一点
轴上找一点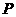 ,使它与点
,使它与点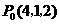 的距离为
的距离为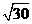 .
.
答案:解:设点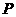 的坐标是
的坐标是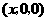 ,由题意,
,由题意,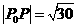 ,即
,即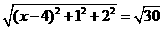 ,
,
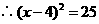 .解得
.解得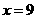 或
或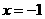 .
.
 点
点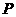 坐标为
坐标为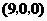 或
或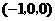 .
.
第10题. 下列各点不在曲线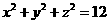 上的是( )
上的是( )
A.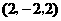 B.
B.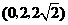 C.
C.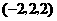 D.
D.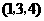
答案:D.
第11题. 坐标原点到下列各点的距离最小的是( )
A.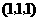 B.
B.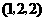 C.
C.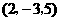 D.
D.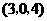
答案:A.
第12题. 已知 点坐标为
点坐标为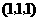 ,
,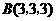 ,点
,点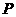 在
在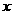 轴上,且
轴上,且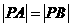 ,则
,则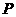 点坐标为( )
点坐标为( )
A.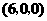 B.
B.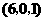 C.
C.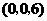 D.
D.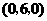
答案:A.
第13题. 在空间直角坐标系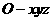 中,
中,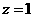 的所有点构成的图形是 .
的所有点构成的图形是 .
答案:过点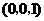 且与
且与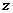 轴垂直的平面
轴垂直的平面
第14题. 点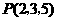 到平面
到平面 的距离为 .
的距离为 .
答案: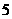
第15题. 求证:以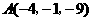 ,
,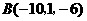 ,
,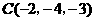 为顶点的三角形是等腰直角三角形.
为顶点的三角形是等腰直角三角形.
答案:证明: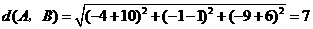 ,
,
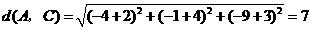 ,
,
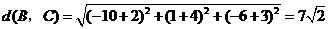 ,
,

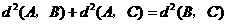 且
且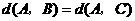 .
.
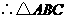 为等腰直角三角形.
为等腰直角三角形.
第16题. 已知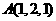 ,
,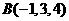 ,
,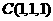 ,
,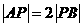 ,则
,则
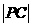 长为 .
长为 .
答案: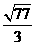 .
.
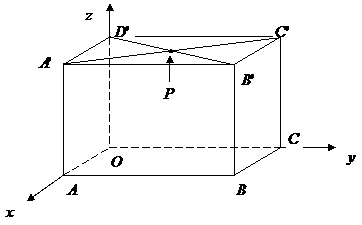
第17题. 如图,长方体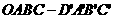 中,
中,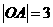 ,
,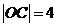 ,
,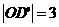 ,
, 于
于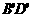 相交于点
相交于点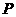 .分别写出
.分别写出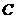 ,
,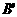 ,
,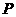 的坐标.
的坐标.
答案: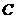 ,
, ,
,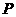 各点的坐标分别是
各点的坐标分别是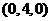 ,
,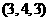 ,
,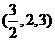 .
.
第18题. 在 平面内的直线
平面内的直线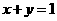 上确定一点
上确定一点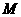 ;使
;使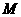 到点
到点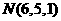 的距离最小.
的距离最小.
答案:解:设点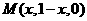 则
则
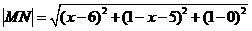
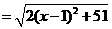
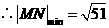 .
.
第19题. 试解释方程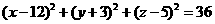 的几何意义.
的几何意义.
答案:该方程几何意义是:在空间中以点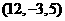 为球心,球半径长为6的球面.
为球心,球半径长为6的球面.
第20题. 点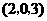 在空间直角坐标系中的位置是在( )
在空间直角坐标系中的位置是在( )
A.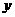 轴上 B.
轴上 B. 平面上 C.
平面上 C. 平面上 D.第一卦限内
平面上 D.第一卦限内
答案:C.
第21题. 点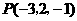 关于平面
关于平面 的对称点是 ,关于平面
的对称点是 ,关于平面 的对称点是 ,关于平面
的对称点是 ,关于平面 的对称点是 ,关于
的对称点是 ,关于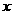 轴的对称点是 ,关于
轴的对称点是 ,关于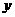 轴的对称点是 ,关于
轴的对称点是 ,关于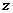 轴的对称点是 .
轴的对称点是 .
答案: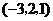 ,
,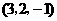 ,
,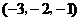 ,
,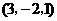 ,
,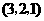 ,
,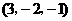 .
.
第22题. 点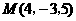 到原点的距离
到原点的距离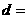 ,到
,到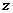 轴的距离
轴的距离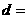 .
.
答案: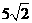 ,
,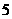 .
.
第23题. 已知两点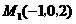 ,
,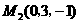 ,此两点间的距离为( )
,此两点间的距离为( )
A.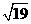 B.
B.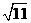 C.
C.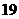 D.
D.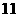
答案:A.
第24题. 若向量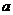 在
在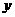 轴上的坐标为
轴上的坐标为 ,其他坐标不为
,其他坐标不为 ,那么与向量
,那么与向量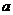 平行的坐标平面是( )
平行的坐标平面是( )
A. 平面 B.
平面 B. 平面 C.
平面 C. 平面 D.以上都有可能
平面 D.以上都有可能
答案:B.
第25题. 在空间直角坐标系中,在 轴上的点
轴上的点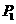 的坐标特点为 ,在
的坐标特点为 ,在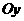 轴上的点
轴上的点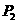 的坐标特点为 ,在
的坐标特点为 ,在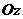 轴上的点
轴上的点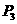 的坐标特点为 ,在
的坐标特点为 ,在 平面上的点
平面上的点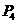 的坐标特点为 ,在
的坐标特点为 ,在 平面上的点
平面上的点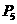 的坐标特点为 ,在
的坐标特点为 ,在 平面上的点
平面上的点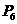 的坐标特点为 .
的坐标特点为 .
答案: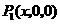 ,
,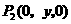 ,
,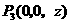 ,
,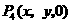 ,
,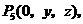
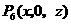 .
.
第26题. 已知空间三点的坐标为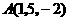 ,
,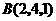 ,
,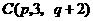 ,若
,若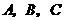 三点共线,则
三点共线,则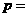 ,
,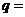 .
.
答案: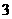 ,
,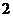
第27题. 已知点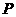 的坐标为
的坐标为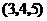 ,试在空间直角坐标系中作出点
,试在空间直角坐标系中作出点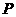 .
.
答案:解:由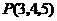 可知点
可知点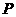 在
在 轴上的射影为
轴上的射影为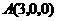 ,在
,在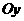 轴上射影为
轴上射影为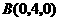 ,以
,以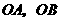 为邻边的矩形
为邻边的矩形 的顶点
的顶点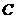 是点
是点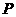 在
在 坐标平面上的射影,
坐标平面上的射影,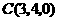 .
.
过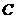 作直线垂直于
作直线垂直于 坐标平面,并在此直线的
坐标平面,并在此直线的 平面上方截取
平面上方截取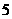 个单位,
个单位,
得到的就是点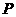 .
.
20.甲、乙两公司生产同一种新产品,经测算,对于函数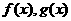 及任意的
及任意的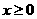 ,当甲公司投入x万元作宣传时,若乙公司投入的宣传费小于
,当甲公司投入x万元作宣传时,若乙公司投入的宣传费小于 万元,则乙公司有失败的风险,否则无失败风险;当乙公司投入x万元作宣传时,若甲公司投入的宣传费小于
万元,则乙公司有失败的风险,否则无失败风险;当乙公司投入x万元作宣传时,若甲公司投入的宣传费小于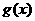 万元,则甲公司有失败的风险,否则无失败风险。w.w.^w.k.s.5*
万元,则甲公司有失败的风险,否则无失败风险。w.w.^w.k.s.5*
(1)请解释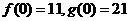 的实际意义;w.w.^w.k.s.5*
的实际意义;w.w.^w.k.s.5*
(2)当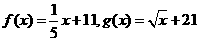 时,甲、乙两公司为了避免恶性竞争,经过协商,同意在双方均无失败风险的情况下尽可能少地投入宣传费,问此时甲、乙两公司各应投入多少宣传费?w.w.^w.k.s.5*
时,甲、乙两公司为了避免恶性竞争,经过协商,同意在双方均无失败风险的情况下尽可能少地投入宣传费,问此时甲、乙两公司各应投入多少宣传费?w.w.^w.k.s.5*

绵阳中学高2012级下学期入学考试题
19.若数列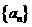 的前n次和是
的前n次和是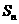 ,点
,点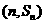
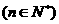 在二次函数
在二次函数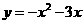 的图象上;数列
的图象上;数列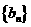 是正项数列,且点
是正项数列,且点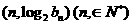 在直线y=x+1上。w.w.^w.k.s.5*
在直线y=x+1上。w.w.^w.k.s.5*
(1)求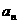 和
和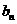 。
。
(2)设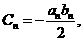 求数列
求数列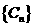 的前n项和
的前n项和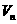 。w.w.^w.k.s.5*
。w.w.^w.k.s.5*
18.已知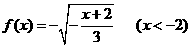 w.w.^w.k.s.5*
w.w.^w.k.s.5*
(1)判断函数 在定义域上的单调性。w.w.^w.k.s.5*
在定义域上的单调性。w.w.^w.k.s.5*
(2)若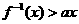 恒成立,求a的范围。
恒成立,求a的范围。

17.已知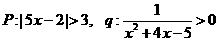 w.w.^w.k.s.5*
w.w.^w.k.s.5*
(1)试判断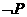 是
是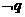 的什么条件。
的什么条件。
(2)设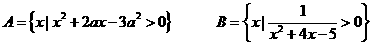
若A B,求a的范围。
B,求a的范围。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com