7．函数模型类

这个问题是指在问题中给出函数关系式，关系式中有的带有需确定的参数，这些参数需要根据问题的内容或性质来确定之后，然后使问题本身获解．

[例8]　 某工厂今年1月、2月、3月生产某产品分别为1万件、1.2万件、1.3万件．为了估测以后每个月的产量，以这三个月的产品数量为依据，用一个函数模拟该产品的月产品的月产量y与月份数x的关系，模拟函数可以选用二次函数或函数y=ab^x+c(其中a、b、c为常数)，已知4月份该产品的产量为1.37万件，请问用以上哪个函数作为模拟函数较好，并说明理由．

解　 设二次函数y₁＝f(x)=px²+qx+x(p≠0)

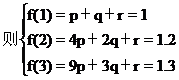
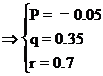
∴y₁=f(x)=－0.05x²+0.35x+0.7

f(4)=－0.05×16+0.35×4+0.7=1.3

又y=ab^x+c

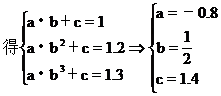
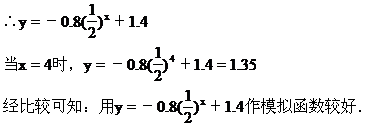
[例9]　 有甲乙两种产品，生产这两种产品所能获得的利润依次

投入3万元资金生产甲、乙两种产品，为获得最大利润，对甲、乙两种产品的资金投入分别应为多少？最大利润是多少？

解 　设投入甲产品资金为x万元，投入乙产品资金为(3－x)万元，总利润为y万元．

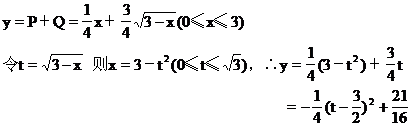
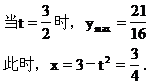
答 　对甲、乙产品分别投资为0.75万元和2.25万元，获最大利润为

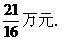
6．复利问题类

复利是一种计算利率的方法，即把前一期的利息和本金加在一起做本金，再计算下一期的利息．设本金为P，每期利率为r，设本利和为y，存期为x，则复利函数式为y=P(1+r)^x．

[例7]　 某企业计划发行企业债券，每张债券现值500元，按年利率6.5%的复利计息，问多少年后每张债券一次偿还本利和1000元？(参考lg2=0.3010，lg1.065＝0.0274)．

解 　设n年后每张债券一次偿还本利和1000元，由1000=500(1+6.5%)ⁿ，解得n=lg2/lg1.065≈11．

答 　11年后每张债券应一次偿还本利和1000元．

5．单利问题类

单利是指本金到期后的利息不再加入本金计算．设本金为P元，每期利率为r，经过n期后，按单利计算的本利和公式为S_n=P(1+nR)．

[例6]　 某人于1996年6月15日存入银行1000元整存整取定期一年储蓄，月息为9‰，求到期的本利和为多少？

解 　这里P=1000元，r=9‰，n＝12，由公式得S₁₂＝P(1+12r)＝1000×(1+0.009×12)=1108元．

答 　本利和为1108元．

4．营销问题类

这类问题是指在营销活动中，计算产品成本、利润(率)，确定销售价格．考虑销售活动的盈利、亏本等情况的一类问题．在营销问题中，应掌握有关计算公式：利润=销售价－进货价．

[例5]　 将进货价为8元的商品按每件10元售出，每天可销售200件，若每件售价涨价0.5元，其销售量就减少10件．问应将售价定为多少时，才能使所赚利润最大，并求出这个最大利润．

解　 设每件售价提高x元，则每件得利润(2+x)元，每天销售量变为(200－20x)件，所获利润

y=(2+x)(200－20x)

=－20(x－4)²+720

当x=4时，即售价定为14元时，每天可获最大利润为720元．

3．工程设计问题类

工程设计问题是指运用数学知识对工程的定位、大小、采光等情况进行合理布局、计算的一类问题．

[例3]　 要在墙上开一个上部为半圆，下部为矩形的窗户(如图2．9－2所示)，在窗框为定长l的条件下，要使窗户透光面积最大，窗户应具有怎样的尺寸？

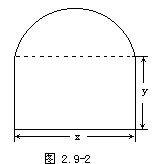
解　 设半圆的直径为x，矩形的高度为y，窗户透光面积为S，则

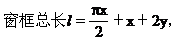
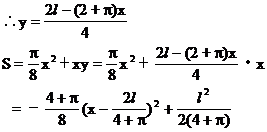
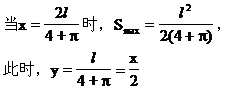
面积最大．

说明 　应用二次函数解实际问题，关键是设好适当的一个变量，建立目标函数．

[例4]　 要使火车安全行驶，按规定，铁道转弯处的圆弧半径不允许小于600米，如果某段铁路两端相距156米，弧所对的圆心角小于180°，试确定圆弧弓形的高所允许的取值范围．

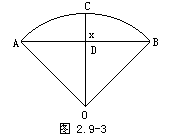
解 　设园的半径为R，圆弧弓形高CD=x(m)．

在Rt△BOD中，DB＝78，OD=B－x

∴(R－x)²+78²=R²

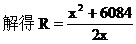
由题意知R≥600

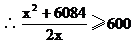
得x²－1200x+6084≥0(x＞0)，解得x≤5.1或x≥1194.9(舍)

∴圆弧弓形高的允许值范围是(0，5.1]．

2．行程问题类

[例2]　 已知，A、B两地相距150公里，某人开汽车以60公里/小时的速度从A地到达B地，在B地停留一小时后再以50公里/小时的速度返回A地，求汽车离开A地的距离x表示为时间t的函数．

解　 根据题意：

(1)汽车由A到B行驶t小时所走的距离x=60t，(0≤t≤2.5)

(2)汽车在B地停留1小时，则B地到A地的距离x＝150(2.5＜x≤3.5)

(3)由B地返回A地，则B地到A地的距离x=150－50(t－3.5)＝325－50t(3.5＜x≤6.5)

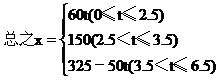
1．几何问题类

用函数思想解决几何(如平面几何、立体几何及解析析几何)问题，这是常常出现的数学本身的综合运用问题．

[例1]　 如图2．9－1，一动点P自边长为1的正方形ABCD的顶点A出发，沿正方形的边界运动一周，再回到A点．若点P的路程为x，点P到顶点A的距离为y，求A、P两点间的距离y与点P的路程x之间的函数关系式．

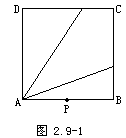
解　 (1)当点P在AB上，即0≤x≤1时，AP＝x，也就是y＝x．

(2)当点P在BC边上，即1＜x≤2时，AB=1，AB+BP＝x，BP＝x－1，根据勾股定理，得AP²＝AB²+BP²

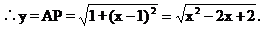
(3)当点P在DC边上，即2＜x≤3时，AD＝1，DP＝3－x．根据勾股定理，得AP²=AD²+DP²．

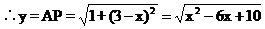
(4)当点P在AD边上，即3＜x≤4时，有y=AP＝4－x．

∴所求的函数关系式为

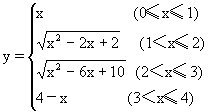
解法二　 设S_x＝Ax²+Bx(x∈N)

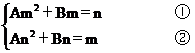
①－②，得A(m²－n²)+B(m－n)＝n－m

∵m≠n　 ∴ A(m+n)+B=－1

故A(m+n)²+B(m+n)＝－(m+n)

即S_m+n＝－(m+n)

说明　 a₁，d是等差数列的基本元素，通常是先求出基本元素，再

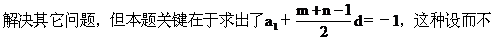
解的“整体化”思想，在解有关数列题目中值得借鉴．解法二中，由于是等差数列，由例22，故可设S_x=Ax²+Bx．(x∈N)

[例14]　 在项数为2n的等差数列中，各奇数项之和为75，各偶数项之和为90，末项与首项之差为27，则n之值是多少？

解　 ∵S_偶项－S_奇项=nd

∴nd=90－75=15

又由a_2n－a₁＝27，即(2n－1)d=27

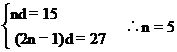
[例15]　 在等差数列{a_n}中，已知a₁＝25，S₉＝S₁₇，问数列前多少项和最大，并求出最大值．

解法一　 建立S_n关于n的函数，运用函数思想，求最大值．

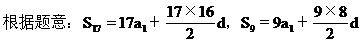
∵a₁=25，S₁₇＝S₉　 解得d＝－2

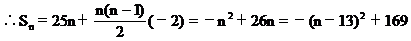
∴当n=13时，S_n最大，最大值S₁₃＝169

解法二　 因为a₁=25＞0，d＝－2＜0，所以数列{a_n}是递减等

∵a₁＝25，S₉＝S₁₇

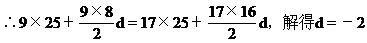
∴a_n=25+(n－1)(－2)=－2n+27

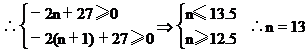
即前13项和最大，由等差数列的前n项和公式可求得S₁₃=169．

解法三　 利用S₉=S₁₇寻找相邻项的关系．

由题意S₉=S₁₇得a₁₀+a₁₁+a₁₂+…+a₁₇=0

而a₁₀+a₁₇=a₁₁+a₁₆=a₁₂+a₁₅=a₁₃+a₁₄

∴a₁₃+a₁₄＝0，a₁₃=－a₁₄　 ∴a₁₃≥0，a₁₄≤0

∴S₁₃=169最大．

解法四　 根据等差数列前n项和的函数图像，确定取最大值时的n．

∵{a_n}是等差数列

∴可设S_n＝An²+Bn

二次函数y=Ax²+Bx的图像过原点，如图3．2－1所示

∵S₉＝S₁₇，

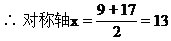
∴取n=13时，S₁₃＝169最大

2．7　 对数·例题解析

[例1]　 计算：

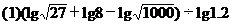
(2)lg²2+lg4·lg50+lg²50

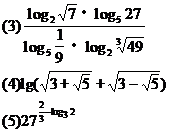
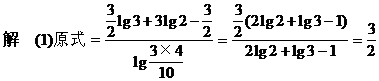
(2)原式=lg²2+2lg2·(1+lg5)+(1+lg5)²=(lg2+1+lg5)²=4

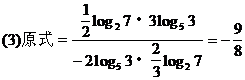
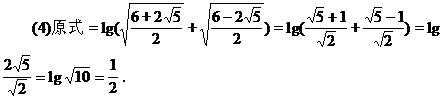
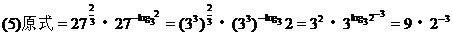
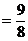
[例2]　 (1)已知10^x＝2，10^y=3，求100^2x-y的值．

(2)已知log₈9=a，log₂5＝b，用a、b表示lg3．

解　 (1)∵10^x＝2∴lg2＝x，∵10^y=3∴lg3=y则100^2x-y=

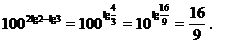
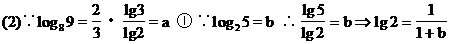
②

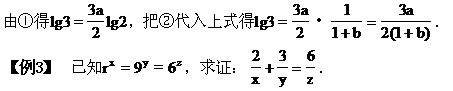
证　 设8^x＝9^y＝6^z＝k(k＞0，且k≠1)则x=log₈k，y＝log₉k，z＝log₆k，

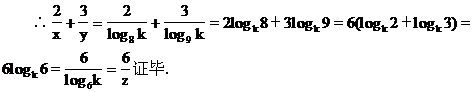
2．4　 反函数·例题解析

[例1]求下列函数的反函数：

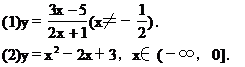
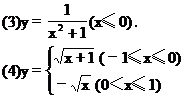
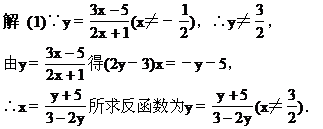
解　 (2)∵y＝(x－1)²+2，x∈(－∞，0]其值域为y∈[2，+∞)，

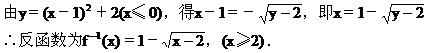
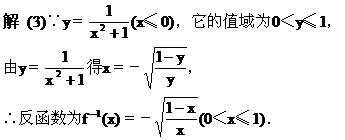
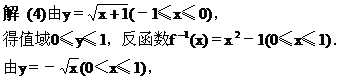
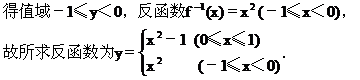
[例2]求出下列函数的反函数，并画出原函数和其反函数的图像．

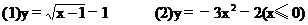
解　 (1)∵已知函数的定义域是x≥1，∴值域为y≥－1，

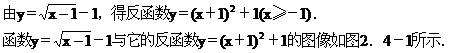
解　 (2)由y＝－3x²－2(x≤0)得值域y≤－2，

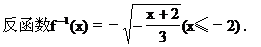
它们的图像如图2．4－2所示．

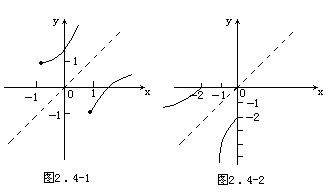
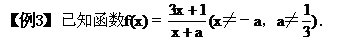
(1)求它的反函数；(2)求使f^-1(x)＝f(x)的实数a的值．

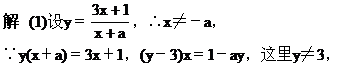
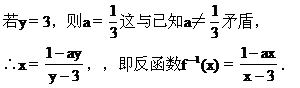
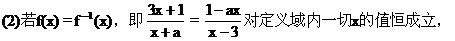
令x＝0，∴a＝－3．

或解 　由f(x)＝f^-1(x)，那么函数f(x)与f^-1(x)的定义域和值域相同，定义域是{x|x≠a，x∈R}，值域y∈{y|y≠3，y∈R}，∴－a＝3即a＝－3．

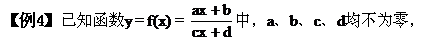
试求a、b、c、d满足什么条件时，它的反函数仍是自身．

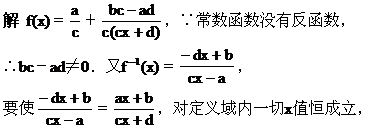
令x＝0，得－a＝d，即a+d＝0．

事实上，当a+d＝0时，必有f^-1(x)＝f(x)，

因此所求的条件是bc－ad≠0，且a+d＝0．

[例5]设点M(1，2)既在函数f(x)＝ax²+b(x≥0)的图像上，又在它的反函数图像上，(1)求f^-1(x)，(2)证明f^-1(x)在其定义域内是减函数．

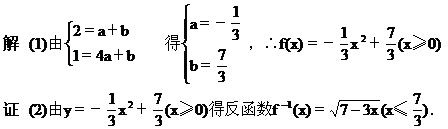
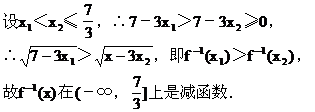
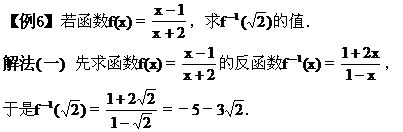
解法(二)　 由函数y＝f(x)与其反函数y＝f^-1(x)之间的一一对应关

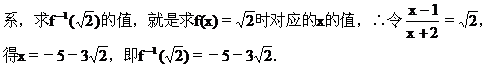
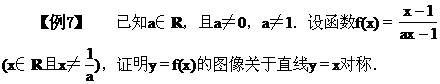
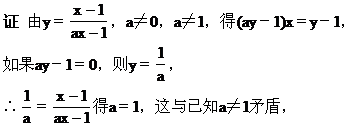
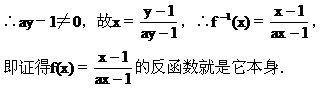
因为原函数的图像与其反函数的图像关于直线y＝x对称，

∴函数y＝f(x)的图像关于直线y＝x对称．