
题目列表(包括答案和解析)
5.在正方体A1B1C1D1-ABCD中,M、N分别是棱A1A和B1B的中点,若θ为直线CM与D1N所成的角,则sinθ等于 ( )
A. 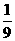 B.
B.
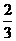 C.
C.
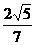 D.
D. 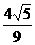
4.已知棱长都相等的正三棱锥内接于一个球,某人画出四个过球心的平面截球与正三棱锥所得的图形如下,则 ( )
A.以下四个图形都是正确的 B.只有(2)(4)是正确的
C.只有(4)是正确的 D.只有(1)(2)是正确的
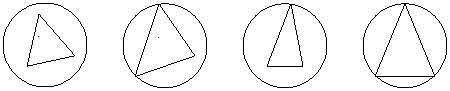
① ② ③ ④
3.已知正方体ABCD-A1B1C1D1的棱长为a,长为定值的线段EF在棱AB上移动(EF<a),若P是A1D1上的定点,Q是C1D1上的动点,则四面体PQEF的体积是 ( )
A.有最小值的一个变量 B.有最大值的一个变量
C.没有最值的一个变量 D.是一个常量
2.已知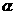 ∥
∥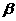 ,
,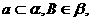 则在
则在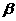 内过点
内过点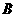 的所有直线中
(
)
的所有直线中
(
)
A.不一定存在与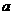 平行的直线 B.只有两条与
平行的直线 B.只有两条与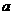 平行的直线
平行的直线
C.存在无数条与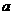 平行的直线 D.存在唯一一条与
平行的直线 D.存在唯一一条与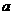 平行的直线
平行的直线
1.两两互相平行的直线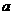 、
、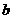 、
、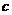 可以确定平面的个数是
(
)
可以确定平面的个数是
(
)
A.1或3 B.1 C.3 D.4
13、已知PA⊥正方形ABCD,PA=AB=2,M,N为BC,CD中点,
⑴求C到面PAM的距离,⑵求BD到面PMN的距离。
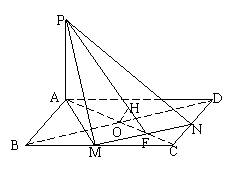 解:延长AM,作CE⊥AM于E
解:延长AM,作CE⊥AM于E
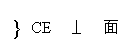 ∵PA⊥正方形ABCD,
∵PA⊥正方形ABCD,
∴PA⊥CE
∵CE⊥AM
∵AB=2,BM=1,CM=1
∴AM=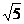 ,
,
∴CE=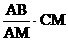 =
=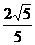
∴C到平面PAM的距离为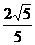
连AC交BD于O,交MN于F,连PF,过O作OH⊥PF
∵M,N为BC,CD中点,
∴MN∥BD
∴BD∥平面PMN,
∴O到平面PMN的距离即为BD到平面PMN的距离。
∵BD⊥AC,MN∥BD ∵PA⊥面ABCD
∴MN⊥AC, ∴PA⊥MN
 ∴MN⊥平面PAC
∴MN⊥平面PAC
∴MN⊥OH
∵OH⊥PF
∵PA=2,AC=2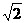 ,AF=
,AF=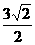 ,OF=
,OF=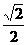
∴PF=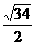 ∴OH=
∴OH=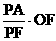 =
=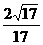
12、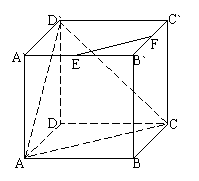 已知正方体ABCD-A`B`C`D`中,E,F分别是A`B`,B`C`的中点。
已知正方体ABCD-A`B`C`D`中,E,F分别是A`B`,B`C`的中点。
求证:EF∥面AD`C。
证明:连A`C`,由E,F分别为A`B`,B`C`的中点
则EF∥A`C`,
又∵A`C`∥AC,
∴EF∥AC
∵AC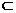 面AD`C
面AD`C
∴EF∥面AD`C
11、a,b为异面直线,且a,b所成角为40°,直线c与a,b均异面,且所成角均为θ,若这样的c共有四条,则θ的范围为 (70°,90°) 。
10、三个平面α,β,γ将空间分成七部分,且α∩β=a,β∩γ=b,则a与b的位置关系为 平行 。
9、在空间四边形ABCD中,E,H分别是AB,AD的中点,F,G为CB,CD上的点,且CF∶CB=CG∶CD=2∶3,若BD=6cm,梯形EFGH的面积 28cm2,则EH与FG间的距离为 8cm 。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com