
题目列表(包括答案和解析)
4.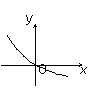
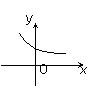
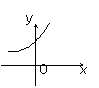
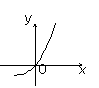 已知函数f(x)=2x,
则f(1-x)的图象为
( )
已知函数f(x)=2x,
则f(1-x)的图象为
( )
A B C D
3、已知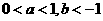 ,则函数
,则函数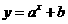 的图像必定不经过( )
的图像必定不经过( )
A、第一象限 B、第二象限 C、第三象限 D、第四象限
2. 设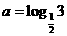 ,
,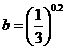 ,
,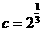 ,则( )
,则( )
A.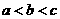 B.
B.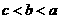 C.
C.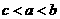 D.
D.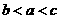
1、已知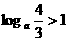 ,则
,则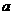 的取值范围是 ( )
的取值范围是 ( )
A. 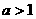 B.
B.
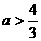 C.
C. 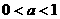 D.
D.
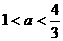
18.(14分)已知函数f(x)=x-2m2+m+3(m∈Z)为偶函数,且f(3)<f(5).
(1)求m的值,并确定f(x)的解析式;
(2)若g(x)=loga(f(x)-ax)(a>0,a≠1),是否存在实数a,使g(x)在区间[2,3]上为增函数.
[解析] (1)由f(3)<f(5),得3-2m2+m+3<5-2m2+m+3⇒-2m2+m+3<1=0.
∵y=x在(-∞,+∞)上为减函数,
∴-2m2+m+3>0⇒-1<m<.
∵m∈Z,∴m=0或m=1.
当m=0时,-2m2+m+3=3,y=x3是奇函数,舍去;
当m=1时,-2m2+m+3=2.
∵f(x)为偶函数,∴f(x)=x2.
(2)假设存在实数a,使g(x)=loga(x2-ax)在区间[2,3]上为增函数,则由g(2)与g(3)存在,得⇒a<2.
令h(x)=x2-ax,则h(x)开口向上,
对称轴x=<1.
∵x∈[2,3]时,h(x)为增函数,又由g(x)=logah(x)在区间[2,3]上为增函数,得a>1,∴1<a<2.
17.(12分)已知函数f(x)=lg(1+x)+lg(1-x).
(1)求函数f(x)的定义域;
(2)判断函数f(x)的奇偶性;
(3)若f(x)=lg g(x),判断函数g(x)在(0,1)内的单调性并用定义证明.
[解析] (1)由得-1<x<1,
∴函数f(x)的定义域为(-1,1).
(2)定义域关于原点对称,对于任意的x∈(-1,1),
有-x∈(-1,1),
f(-x)=lg(1-x)+lg(1+x)=f(x),
∴f(x)为偶函数.
(3)∵f(x)=lg(1-x2)=lg g(x),∴g(x)=1-x2.
对任意的0<x1<x2<1,有
g(x1)-g(x2)=(1-x12)-(1-x22)
=(x1+x2)(x2-x1)>0.
即g(x1)>g(x2),∴g(x)在(0,1)内单调递减.
16.(12分)已知x∈[-3,2],求f(x)=-+1的最小值与最大值.
[解析] 设=t,即x=t,
∵x∈[-3,2],∴≤t≤8.
∵f(t)=t2-t+1=2+,
又∵≤t≤8,
∴当t=,即x=1时,f(x)有最小值;
当t=8,即x=-3时,f(x)有最大值57.
15.(12分)(1)-(-2009)0--+-2
(2)log2.56.25+lg0.001+ln+2-1+log23.
[解析] (1)原式=-1-+=
(2)原式=2-3++×3=1
14.设x∈(0,1)时,y=xp(p∈R)的图象在直线y=x的上方,则p的取值范围是________.
[解析] 结合幂函数的图象可知p<1.
[答案] p<1
13.设a=lg e,b=(lg e)2,c=lg,则a,b,c的从大到小的顺序是________>________>________.
[解析] ∵1<e<3,则1<<e<e2<10,
∴0<lg e<1.则lg=lg e<lg e,
即c<a.又0<lg e<1,
∴(lg e)2<lg e,即b<a.同时
c-b=lg e-(lg e)2=lg e[1-2lg e]
=lg e·lg>0.
∴c>b.
[答案] a,c,b
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com