
7.由四个大小相同的正方体组成的集合体如图所示,那么它的左视图是( )

A B C D
6.如图,⊙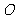 是
是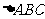 的外接圆,
的外接圆,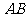 是直径,若
是直径,若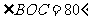 ,则
,则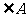 等于( )
等于( )
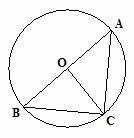
A.60º B.50º C.40º D.30º
5.下列调查中,适宜采用全面调查(普查)方式的是( )
A.调查一批新型节能灯泡的使用寿命
B.调查长江流域的水污染情况
C.调查重庆市初中学生的视力情况
D.为保证“神舟7号”的成功发射,对其零部件进行检查
4.如图,直线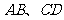 相交于点
相交于点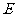 ,
,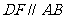 ,若
,若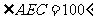 ,则
,则 等于( )
等于( )
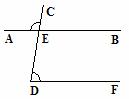
A.70º B.80º C.90º D.100º
3.函数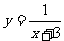 的自变量取值范围是( )
的自变量取值范围是( )
A. B.
B.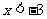 C.
C. D.
D.
2.计算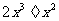 的结果是( )
的结果是( )
A.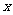 B.
B.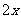 C.
C.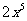 D.
D.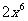
1.-5的相反数是( )
A.5 B.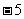 C.
C.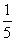 D.
D.
26.(本小题10分)
已知函数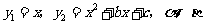 为方程
为方程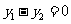 的两个根,点
的两个根,点 在函数
在函数 的图象上。
的图象上。
(Ⅰ)若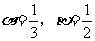 ,求函数
,求函数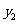 的解析式;
的解析式;
(Ⅱ)在(Ⅰ)的条件下,若函数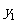 与
与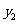 的图象的两个交点为
的图象的两个交点为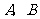 ,当
,当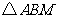 的面积为
的面积为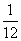 时,求
时,求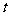 的值;
的值;
(Ⅲ)若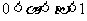 ,当
,当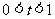 时,试确定
时,试确定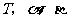 三者之间的大小关系,并说明理由.
三者之间的大小关系,并说明理由.
25.(本小题10分)
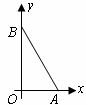
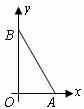
已知一个直角三角形纸片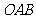 ,其中
,其中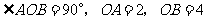 .如图,将该纸片放置在平面直角坐标系中,折叠该纸片,折痕与边
.如图,将该纸片放置在平面直角坐标系中,折叠该纸片,折痕与边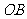 交于点
交于点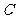 ,与边
,与边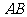 交于点
交于点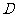 。
。
(Ⅰ)若折叠后使点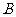 与点
与点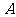 重合,求点
重合,求点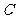 的坐标;
的坐标;
(Ⅱ)若折叠后点 落在边
落在边 上的点为
上的点为 ,设
,设 ,
, ,试写出
,试写出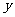 关于
关于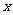 的函数解析式,并确定
的函数解析式,并确定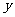 的取值范围;
的取值范围;
(Ⅲ)若折叠后点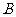 落在边
落在边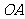 上的点为
上的点为 ,且使
,且使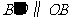 ,求此时点
,求此时点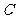 的坐标.
的坐标.
24.(本小题8分)
注意:为了使同学们更好地解答本题,我们提供了一种解题思路,你可以依照这个思路填空,并完成本题解答的全过程.如果你选用其他的解题方案,此时,不必填空,只需按照解答题的一般要求,进行解答即可。
如图①,要设计一幅宽20cm,长30cm的矩形图案,其中有两横两竖的彩条,横、竖彩条的宽度比为2∶3,如果要使所有彩条所占面积为原矩形图案面积的三分之一,应如何设计每个彩条的宽度?
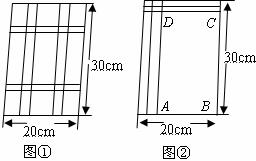
分析:由横、竖彩条的宽度比为2∶3,可设每个横彩条的宽为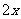 ,则每个竖彩条的宽为
,则每个竖彩条的宽为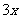 .为更好地寻找题目中的等量关系,将横、竖彩条分别集中,原问题转化为如图②的情况,得到矩形
.为更好地寻找题目中的等量关系,将横、竖彩条分别集中,原问题转化为如图②的情况,得到矩形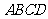 。
。
结合以上分析完成填空:如图②,用含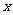 的代数式表示:
的代数式表示:
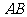 =____________________________cm;
=____________________________cm;
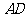 =____________________________cm;
=____________________________cm;
矩形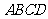 的面积为_____________cm
的面积为_____________cm ;
;
列出方程并完成本题解答。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com