
4.据《宁波市休闲基地和商务会议基地建设五年行动计划》,预计到2012年,宁波市接待游客容量将达到4640万人,其中4640万用科学记数法可表示为 ( )
A.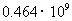 B.
B.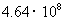 C.
C.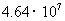 D.
D.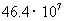
3.一个不透明的布袋装有4个只有颜色的球,其中2个红色,1个白色,1个黑色,搅匀后从布袋里摸出1个球,摸到红球的概率是 ( )
A.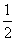 B.
B.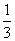 C.
C.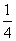 D.
D.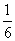
2.等腰直角三角形的一个底角的度数是 ( )
A.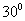 B.
B.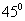 C.
C.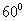 D.
D.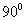
1.下列四个数中,比0小的数是 ( )
A.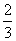 B.
B.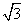 C.
C.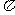 D.
D.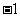
24.如图,已知直线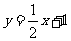 与
与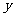 轴交于点A,与
轴交于点A,与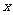 轴交于点D,抛物线
轴交于点D,抛物线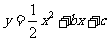 与直线交于A、E两点,与
与直线交于A、E两点,与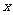 轴交于B、C两点,且B点坐标为 (1,0)。
轴交于B、C两点,且B点坐标为 (1,0)。
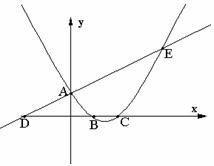
(1)求该抛物线的解析式;
(2)动点P在轴上移动,当△PAE是直角三角形时,求点P的坐标P。
(3)在抛物线的对称轴上找一点M,使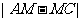 的值最大,求出点M的坐标。
的值最大,求出点M的坐标。
23.“六一”前夕,某玩具经销商用去2350元购进A、B、C三种新型的电动玩具共50套,并且购进的三种玩具都不少于10套,设购进A种玩具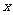 套,B种玩具
套,B种玩具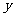 套,三种电动玩具的进价和售价如下表所示,
套,三种电动玩具的进价和售价如下表所示,
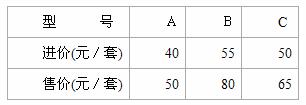
(1)用含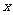 、
、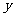 的代数式表示购进C种玩具的套数;
的代数式表示购进C种玩具的套数;
(2)求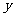 与
与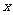 之间的函数关系式;
之间的函数关系式;
(3)假设所购进的这三种玩具能全部卖出,且在购销这种玩具的过程中需要另外支出各种费用200元。
①求出利润P(元)与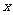 (套)之间的函数关系式;②求出利润的最大值,并写出此时三种玩具各多少套。
(套)之间的函数关系式;②求出利润的最大值,并写出此时三种玩具各多少套。
22.在直角梯形ABCD中,AB∥DC,AB⊥BC,∠A=60°,AB=2CD,E、F分别为AB、AD的中点,连结EF、EC、BF、CF。
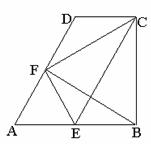
(1)判断四边形AECD的形状(不证明);
(2)在不添加其它条件下,写出图中一对全等的三角形,用符号“≌”表示,并证明。
(3)若CD=2,求四边形BCFE的面积。
21.将正面分别标有数字1、2、3、4、6,背面花色相同的五张卡片沅匀后,背面朝上放在桌面上,从中随机抽取两张。
(1)写出所有机会均等的结果,并求抽出的两张卡片上的数字之和为偶数的概率;
(2)记抽得的两张卡片的数字为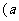 ,
,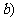 ,求点P
,求点P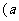 ,
,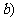 在直线
在直线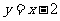 上的概率;
上的概率;
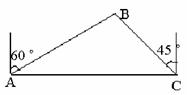
20.海船以5海里/小时的速度向正东方向行驶,在A处看见灯塔B在海船的北偏东60°方向,2小时后船行驶到C处,发现此时灯塔B在海船的北偏西45方向,求此时灯塔B到C处的距离。
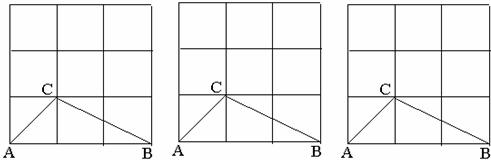
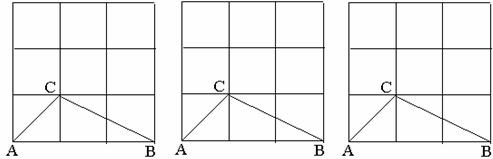
19.在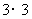 的正方形格点图中,有格点△ABC和△DEF,且△ABC和△DEF关于某直线成轴对称,请在右面的备用图中画出所有这样的△DEF。
的正方形格点图中,有格点△ABC和△DEF,且△ABC和△DEF关于某直线成轴对称,请在右面的备用图中画出所有这样的△DEF。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com