
5.函数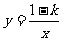 的图象和直线
的图象和直线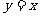 无交点则
无交点则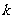 的取值范围是( )
的取值范围是( )
A.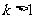 B.
B.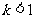 C.
C. D.
D.
4.下列四点中,在反比例函数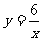 的图象上的是( )
的图象上的是( )
A.(1,-6) B.(2,4) C.(3,-2) D.(-6,-1)
3.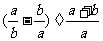 的结果为(
)
的结果为(
)
A.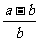 B.
B.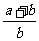 C.
C.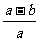 D.
D.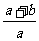
2.若分式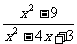 的值为零;则
的值为零;则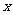 的值( )
的值( )
A.3或-3 B.3 C.-3 D.0
1.在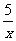 ,
,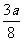 ,
,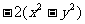 ,
,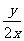 ,
,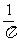 ,
,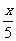 ,
,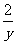 中分式有( )个
中分式有( )个
A.2 B.3 C.4 D.5
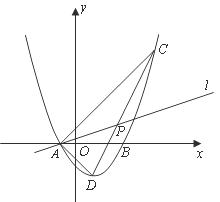
26.如图,在平面直角坐标系中,开口向上的抛物线与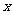 轴交于
轴交于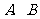 两点,
两点,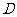 为抛物线的顶点,
为抛物线的顶点,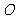 为坐标原点.若
为坐标原点.若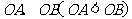 的长分别是方程
的长分别是方程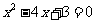 的两根,且
的两根,且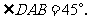
(1)求抛物线对应的二次函数解析式;
(2)过点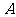 作
作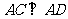 交抛物线于点
交抛物线于点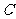 ,求点
,求点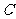 的坐标;
的坐标;
(3)在(2)的条件下,过点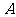 任作直线
任作直线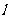 交线段
交线段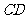 于点
于点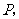 求
求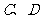 到直线
到直线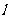 的距离分别为
的距离分别为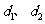 ,试求
,试求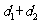 的最大值.
的最大值.
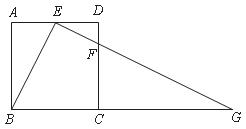
25.如图,在梯形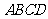 中,
中,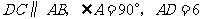 厘米,
厘米,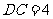 厘米,
厘米,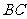 的坡度
的坡度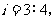 动点
动点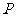 从
从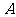 出发以2厘米/秒的速度沿
出发以2厘米/秒的速度沿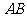 方向向点
方向向点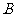 运动,动点
运动,动点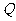 从点
从点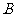 出发以3厘米/秒的速度沿
出发以3厘米/秒的速度沿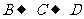 方向向点
方向向点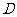 运动,两个动点同时出发,当其中一个动点到达终点时,另一个动点也随之停止.设动点运动的时间为
运动,两个动点同时出发,当其中一个动点到达终点时,另一个动点也随之停止.设动点运动的时间为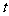 秒.
秒.
(1)求边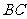 的长;
的长;
(2)当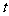 为何值时,
为何值时,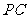 与
与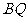 相互平分;
相互平分;
(3)连结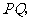 设
设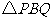 的面积为
的面积为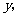 探求
探求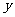 与
与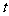 的函数关系式,求
的函数关系式,求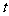 为何值时,
为何值时,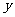 有最大值?最大值是多少?
有最大值?最大值是多少?
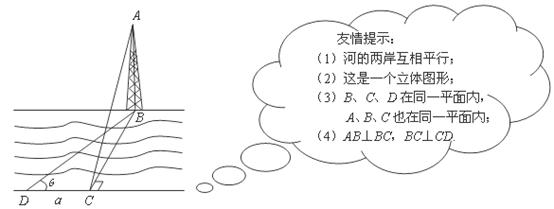
24.如图,某学习小组为了测量河对岸塔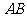 的高度,在塔底部点
的高度,在塔底部点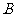 的正对岸点
的正对岸点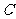 处,测得塔顶点
处,测得塔顶点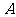 的仰角为
的仰角为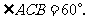
(1)若河宽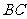 是36米,求塔
是36米,求塔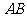 的高度;(结果精确到0.1米)
的高度;(结果精确到0.1米)
(2)若河宽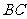 的长度不易测量,如何测量塔
的长度不易测量,如何测量塔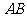 的高度呢?小强思考了一种方法:从点
的高度呢?小强思考了一种方法:从点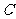 出发,沿河岸前行
出发,沿河岸前行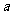 米至点
米至点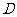 处,若在点
处,若在点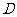 处测出
处测出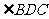 的度数
的度数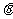 ,这样就可以求出塔
,这样就可以求出塔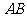 的高度了.
的高度了.
小强的方法可行吗?若行,请用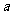 和
和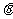 表示塔
表示塔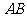 的高度,若不能,请说明理由.
的高度,若不能,请说明理由.
23.本题为选做题,从甲、乙两题中选做一题即可,如果两题都做,只以甲题计分。
甲题:关于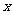 的一元二次方程
的一元二次方程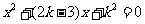 有两个不相等的实数根
有两个不相等的实数根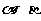 .
.
(1)求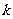 的取值范围;
的取值范围;
(2)若 求
求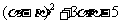 的值.
的值.
乙题:如图(13),在正方形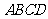 中,
中,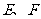 分别是边
分别是边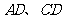 上的点,
上的点,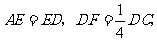 连结
连结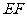 并延长交
并延长交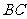 的延长线于点
的延长线于点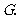
(1)求证: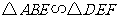 ;
;
(2)若正方形的边长为4,求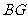 的长.我选做的是___________.
的长.我选做的是___________.
22.一个不透明的口袋里装有红、白、黄三种颜色的乒乓球(除颜色外其余都相同),其中白球有2个,黄球有1个.若从中任意摸出一个球,这个球是白球的概率为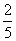 .
.
(1)求口袋中红球的个数;
(2)把口袋中的球搅匀后摸出一个球,放回搅匀再摸出第二个球,求摸到的两个球是一红一白的概率.(请结合树状图或列表加以解答)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com