25．(本题满分10分)

如下图，在△ABC中，∠ACB＝90°，AC＝2，BC＝3，D是BC边上的一点，直线DE⊥BC于点D，交AB于点E，CF∥AB交直线DE于点F，设。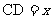

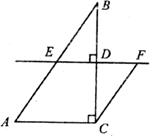
(1)当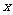取何值时，四边形EACF是菱形？请说明；

(2)当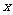取何值时，四边形EACD的面积为2？

24．(本题满分9分)

一只不透明的袋子中装有4个小球，分别标有数字1，2，3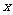，，这些球除数字外其余都相同。甲、乙两人每次同时从袋中各随机摸出一个球，并计算摸出的这两个小球上的数字之和，记录后都将小球放回袋中搅匀，进行重复实验。实验数据如下表：

解答下列问题：

(1)如果实验继续进行下去，根据上表数据，出现“和为7”的频率将稳定在它的概率附近，试估计“和为7”的概率；

(2)根据(1)，若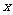是不等于2，3，4的自然数，试求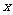的值。

23．(本题10分)

已知在平面直角坐标系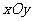中，坐标原点为O，有三个点A(0，－6)，B(－3，0)，C(，2)恰好在同一条直线上。

(1)求图像经过其中一点的反比倒函数的解析式；

(2)求△AOC的面积。

22．(本题满分9分)

已知：如下图，□ABCD中，F，G是边AB上的两个点，且FC平分∠BCD，GD平分∠ADC，FC与GD相交于点E。

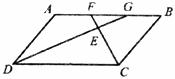
求证：AF＝GB，DG⊥CF。

21．(本题满分9分)

如下图，B，C，E三点在同一条直线上，AC∥DE，AC＝CE，∠ACD＝∠B。

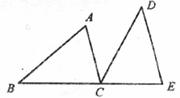
求证：△ABC≌△CDE

20．(本题满分9分)

已知关于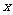的一元二次方程。

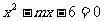(1)若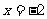是方程的一个根，求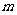的值和方程的另一个根；

(2)对于任意实数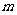，判断方程的根的情况，并说明理由。

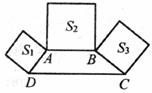
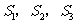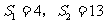19．如下图，梯形ABCD中，AB∥DC，∠ADC+∠BCD＝90°，且DC＝2AB。分别以DA，AB，BC为边向梯形外作正方形，其面积分别为，已知，那么__________。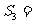

18．在平面直角坐标系中，直线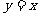向上平移1个单位长度得到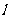直线，直线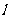与反比例函数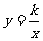的图像的一个交点为A(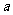，2)，则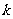的值是__________。

17．在－9，－6，－3，－1，2，3，6，8，11这九个数中，任取一个作为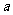值，能够使关于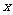的一元二次方程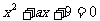有两个实数根的概率是__________。

16．已知一个直角三角形的两条直角边的长恰好是方程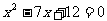的两个根，则这个直角三角形的斜边长为__________。