
1.若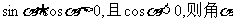 是
是
A.第一象限角 B.第二象限角 C.第三象限角 D.第四象限角
22.(本小题12分)已知函数f(x)=ax3+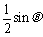 x2-2x+c,过点
x2-2x+c,过点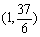 ,且在(-2,1)内单调递减,在[1,
,且在(-2,1)内单调递减,在[1, 上单调递增。
上单调递增。
(1)证明sinθ=1,并求f(x)的解析式。
(2)若对于任意的x1,x2∈[m,m+3](m≥0),不等式|f(x1)-f(x2)|≤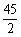 恒成立。试问这样的m是否存在,若存在,请求出m的范围,若不存在,说明理由。
恒成立。试问这样的m是否存在,若存在,请求出m的范围,若不存在,说明理由。
(3)已知数列{an}中,a1∈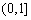 ,an+1=f(an),求证:an+1>8·lnan(n∈N*)。
,an+1=f(an),求证:an+1>8·lnan(n∈N*)。
21.(本小题满分12分)已知双曲线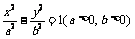 的离心率
的离心率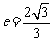 ,过点
,过点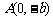 和
和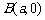 的直线与原点间的距离为
的直线与原点间的距离为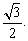
(Ⅰ)求双曲线方程;
(Ⅱ)直线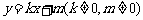 与双曲线交于不同的两点
与双曲线交于不同的两点 ,且
,且 两点都在以
两点都在以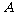 为圆心的同一个圆上,求
为圆心的同一个圆上,求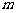 的取值范围.
的取值范围.
20.(本小题满分12分)
已知数列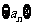 满足
满足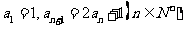
(Ⅰ)求数列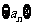 的通项公式;
的通项公式;
(Ⅱ)若数列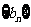 满足
满足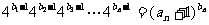 ,证明:
,证明: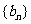 是等差数列;
是等差数列;
(Ⅲ)证明: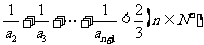
19.(本小题12分)袋中有形状大小完全相同的8个小球,其中红球5个,白球3个。某人逐个从袋中取球,第一次取出一个小球,记下颜色后放回袋中;第二次取出一个小球,记下颜色后,不放回袋中,第三次取出一个小球,记下颜色后,放回袋中,第四次取出一个小球,记下颜色后不放回袋中……,如此进行下去,直到摸完球为止。
(1)求第四次恰好摸到红球的概率;
(2)记ξ为前三次摸到红球的个数,写出其分布列,并求其期望Eξ。
18.(本小题12分)四棱锥P-ABCD中,PA⊥底面ABCD,AB∥CD,AD=CD=1,∠BAD=120°,PA=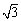 ,∠ACB=90°。
,∠ACB=90°。
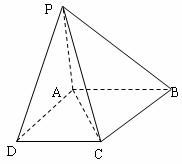
(1)求证:BC⊥平面PAC;
(2)求二面角D-PC-A的大小的正切值;
(3)求点B到平面PCD的距离。
17.(本小题10分)已知向量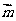 =(1+cosB,sinB)且与向量
=(1+cosB,sinB)且与向量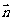 =(0,1)所成的角为
=(0,1)所成的角为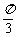 ,其中A、B、C为ΔABC的三个内角。
,其中A、B、C为ΔABC的三个内角。
(1)求角B的大小;(2)若AC=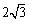 ,求ΔABC周长的最大值。
,求ΔABC周长的最大值。
16.给出下列四个结论:
①若A、B、C、D是平面内四点,则必有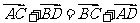 ;
;
②“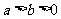 ”是“
”是“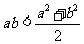 ”的充要条件;
”的充要条件;
③如果函数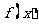 对任意的
对任意的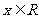 都满足
都满足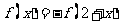 ,则函数
,则函数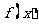 是周期函数;
是周期函数;
④已知点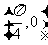 和直线
和直线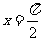 分别是函数
分别是函数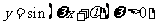 图像的一个对称中心和一条对称轴,则
图像的一个对称中心和一条对称轴,则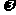 的最小值为2;
的最小值为2;
其中正确结论的序号是 .(填上所有正确结论的序号).
15.已知函数f(x)= 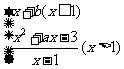 在x=1处连续,则
在x=1处连续,则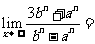 ___
___
14.直三棱柱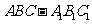 中,
中,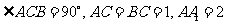 ,则直线
,则直线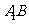 与平面
与平面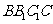 所成角的正切值为 。
所成角的正切值为 。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com