
19.(本小题满分14分)
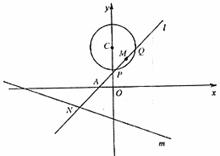
如图,已知定圆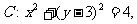 定直线m:x+3y+6=0,过A(-1,0)的一条动直线l与直线m相交于N,与圆C相交于P、Q两点,M是PQ中点。
定直线m:x+3y+6=0,过A(-1,0)的一条动直线l与直线m相交于N,与圆C相交于P、Q两点,M是PQ中点。
(I)已知l过圆心C,求证:l与m垂直;
(II)当|PQ|=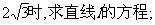
(III)设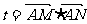 ,试问t是否为定值,若为定值,请求出t的值;若不为定值,请说明理由。
,试问t是否为定值,若为定值,请求出t的值;若不为定值,请说明理由。
18.(本小题满分13分)
甲、乙两运动员进行射击训练,已知他们击中的环数都稳定在8,9,10环,且每次射击成绩互不影响,已知甲、乙射击命中环数的概率如下表:
|
|
8环 |
9环 |
10环 |
|
甲 |
0.2 |
0.45 |
0.35 |
|
乙 |
0.25 |
0.4 |
0.35 |
(I)若甲、乙两运动员各射击一次,求甲运动员击中8环且乙运动员击中9环的概率。
(II)若甲、乙两运动员各自射击两次,求这4次射击中恰有3次击中9环以上(含9环)的概率。
17.(本小题满分14分)
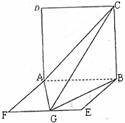
如图,ABCD是边长为2a的正方形,ABEF是矩形,且二面角C-AB-F是直二面角,AF=a,G是EF的中点。
(I)求证:平面AGC⊥平面BGC
(II)求GB与平面AGC所成角的大小;
(III)求二面角B-AC-G的大小。
16.(本小题满分13分)
在等腰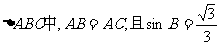 .
.
(I)求cosA的值;
(II)若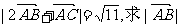 。
。
15.(本小题满分13分)
已知递增的等比例数列{an}满足a2+a3+a4=28,且a3+2是a2+a4的等差中项。
|
(II)若bn=log2 an+1,求数列|bn|的前n项和Sn。
14.已知 当
当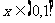 时,
时,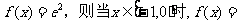 ;当
;当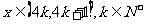 时,f(x)= 。
时,f(x)= 。
13.已知正方体ABCD-A1B1C1D1中,F是AD的中点,C为AB上一点,若CF⊥FG,则∠C1FG的大小是 。
12.直线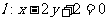 过椭圆的左焦点F1和一个项点B,该椭圆的离心率为
。
过椭圆的左焦点F1和一个项点B,该椭圆的离心率为
。
11.若二项式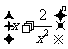 的展开式共7项,则n的值为
,展开式中的常数项为 .
的展开式共7项,则n的值为
,展开式中的常数项为 .
10.若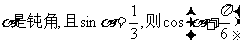 的值为
.
的值为
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com