
1.已知i是虚数单位,实数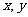 满足
满足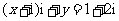 ,则
,则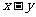 的值为 ( )
的值为 ( )
A.-1 B.0 C.1 D.2
22.(本小题满分14分)设函数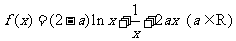 .
.
(Ⅰ)当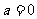 时,求
时,求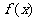 的极值;
的极值;
(Ⅱ)当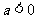 时,求
时,求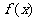 的单调区间;
的单调区间;
(Ⅲ)若对任意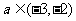 及
及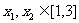 ,恒有
,恒有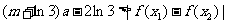 成立,求
成立,求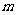 的取值范围.
的取值范围.
21.(本小题满分12分)已知抛物线C: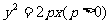 上横坐标为4的点到焦点的距离为5.
上横坐标为4的点到焦点的距离为5.
(Ⅰ)求抛物线C的方程;
(Ⅱ)设直线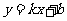 与抛物线C交于两点
与抛物线C交于两点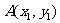 ,
,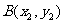 ,且
,且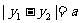
( ,且
,且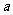 为常数).过弦AB的中点M作平行于
为常数).过弦AB的中点M作平行于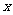 轴的直线交抛物线于点D,连结AD、BD得到
轴的直线交抛物线于点D,连结AD、BD得到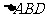 .
.
(ⅰ)求证: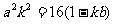 ;
;
(ⅱ)求证: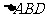 的面积为定值.
的面积为定值.
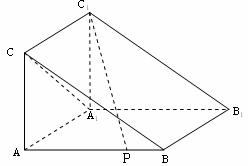
20.(本小题满分12分)如图,在体积为1的三棱柱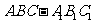 中,侧棱
中,侧棱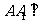 底面
底面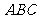 ,
,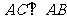 ,
,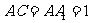 ,
,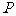 为线段
为线段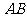 上的动点.
上的动点.
(Ⅰ)求证: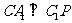 ;
;
(Ⅱ)线段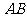 上是否存在一点
上是否存在一点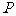 ,使四面体
,使四面体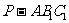 的体积为
的体积为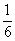 ?若存在,请确定点
?若存在,请确定点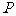 的位置;若不存在,请说明理由.
的位置;若不存在,请说明理由.
19.(本小题满分12分)
已知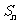 为数列
为数列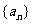 的前
的前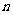 项的和,且
项的和,且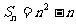 .
.
(Ⅰ)求数列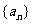 的通项公式;
的通项公式;
(Ⅱ)若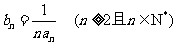 ,记
,记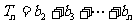 ,求证:
,求证: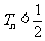 .
.
18.(本小题满分12分)晚会上,主持人前面放着A、B两个箱子,每箱均装有3个完全相同的球,各箱的三个球分别标有号码1,2,3。现主持人从A、B两箱中各摸出一球.
(Ⅰ)若用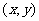 分别表示从A、B两箱中摸出的球的号码,请写出数对
分别表示从A、B两箱中摸出的球的号码,请写出数对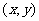 的所有情形,并回答一共有多少种;
的所有情形,并回答一共有多少种;
(Ⅱ)求所摸出的两球号码之和为5的概率;
(Ⅲ)请你猜这两球的号码之和,猜中有奖。猜什么数获奖的可能性大?说明理由.
17.(本小题满分12分)
已知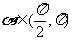 ,且
,且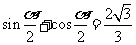 .
.
(Ⅰ)求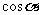 的值;
的值;
(Ⅱ)若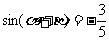 ,
,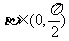 ,求
,求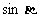 的值.
的值.
16.对任意正整数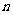 ,定义
,定义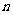 的阶乘
的阶乘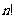 如下:
如下: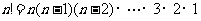 .
.
例如4!=4×3×2×1. 现有四个命题:
①2!×3!= 6!; ② 2009!的个位数字为0;
③(a+b)!=a!+b!(a,b N*); ④n·n!=(n+1)!- n!(n
N*); ④n·n!=(n+1)!- n!(n N*).
N*).
其中所有正确命题的序号是 .
15.已知函数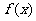 为
为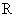 上的奇函数,当
上的奇函数,当 时,
时,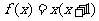 .若
.若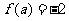 ,则实数
,则实数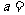 .
.
14.设向量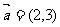 ,b
,b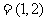 ,若向量λa+ b与向量c
,若向量λa+ b与向量c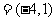 垂直,则λ=
.
垂直,则λ=
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com