
19.(本大题共12分)设函数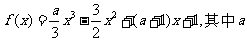 为实数.
为实数.
(Ⅰ)已知函数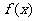 在
在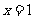 处取得极值,求
处取得极值,求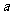 的值;
的值;
(Ⅱ)已知不等式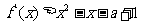 对任意
对任意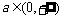 都成立,求实数
都成立,求实数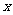 的取值范围.
的取值范围.
18.(本大题共10分)
如图,四棱锥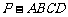 中,
中, 平面
平面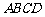 ,底面
,底面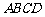 是直角梯形,
是直角梯形,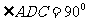 ,
,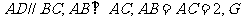 为
为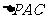 的重心,
的重心,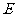 为
为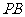 的中点,
的中点,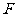 在线段
在线段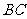 上,且
上,且 .
.
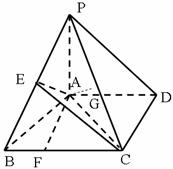
(Ⅰ)求证: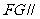 平面
平面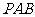 ;
;
(Ⅱ)求证: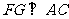 ;
;
(Ⅲ)设二面角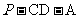 的大小为
的大小为 ,当
,当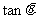 取何值时,
取何值时,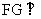 平面
平面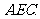
|
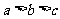 ,求证:
,求证: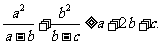
17.(本大题共8分)已知数列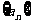 的通项公式是
的通项公式是 ,
,
记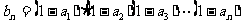
(Ⅰ)写出数列 的前三项;
的前三项;
(Ⅱ)猜测数列 的通项公式,并用数学归纳法给出证明.
的通项公式,并用数学归纳法给出证明.
15.已知函数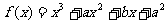 在
在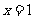 处有极值
处有极值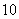 ,则
,则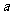 = ;
= ; .
.
14.在三棱锥 中,三条棱
中,三条棱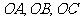 两两互相垂直,且
两两互相垂直,且 是棱
是棱 的中点,则
的中点,则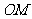 与平面
与平面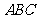 所成角的正切值是 。
所成角的正切值是 。
13.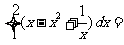 ;
;
12.设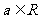 ,若函数
,若函数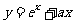 ,
,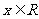 ,有大于零的极值点,则
,有大于零的极值点,则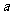 的取值范围是 ;
的取值范围是 ;
11.若复数z=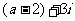 (
(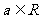 )是纯虚数,则
)是纯虚数,则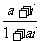 = ;
= ;
10.设函数 的图象上的点
的图象上的点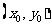 的切线的斜率为
的切线的斜率为 ,若
,若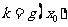 ,则函数
,则函数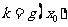 的图象大致为
的图象大致为
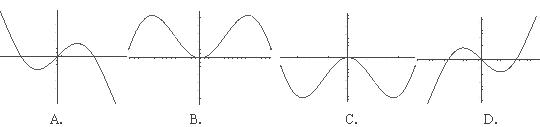
9.设 在
在 内单调递增,
内单调递增,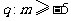 ,则
,则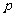 是
是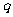 的
的
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分也不必要条件
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com