
20.(本小题满分12分)
某学校课题组为了研究学生的数学成绩与物理成绩之间的关系,随即抽取高二年纪20名学生某次考试成绩(百分制)如下表所示:
|
序号 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
数学成绩 |
95 |
75 |
80 |
94 |
92 |
65 |
67 |
84 |
98 |
71 |
|
物理成绩 |
90 |
63 |
72 |
87 |
91 |
71 |
58 |
82 |
93 |
81 |
|
序号 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
|
数学成绩 |
67 |
93 |
64 |
78 |
77 |
90 |
57 |
83 |
72 |
83 |
|
物理成绩 |
77 |
82 |
48 |
85 |
69 |
91 |
61 |
84 |
78 |
86 |
|
(1)根据上表完成下面的2×2列联表:
|
|
数学成绩优秀 |
数学成绩不优秀 |
合计 |
|
物理成绩优秀 |
|
|
|
|
物理成绩不优秀 |
|
12 |
|
|
合计 |
|
|
20 |
(2)根据题(1)中表格的数据计算,有多少的把握,认为学生的数学成绩与物理成绩之间有关系?
(3)若按下面的方法从这个20个人中抽取1人来了解有关情况:将一个标有数字1,2,3,4,5,6的正六面体骰子连续投掷两次,记朝上的两个数字的乘积为被抽取人的序号,试求:
①抽到12号的概率;②抽到“无效序号(序号大于20)”的概率。
19. (本小题满分12分)
(本小题满分12分)
在平面直角坐标系中,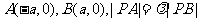 ,其中
,其中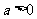 且
且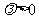 ,求动点
,求动点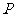 的轨迹方程,并说明轨迹的类型
的轨迹方程,并说明轨迹的类型
18.(本小题满分12分)
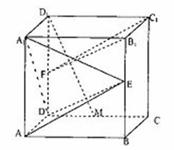
在正方体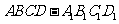 中,
中,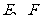 分别为棱
分别为棱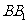 和
和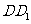 中点。
中点。
(1)求证:平面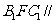 平面
平面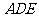 ;
;
(2)试在棱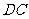 上求一点
上求一点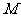 ,使
,使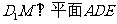
17.(本小题满分12分)已知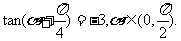
(1)求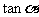 的值;
的值;
 (2)求
(2)求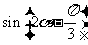 的值。
的值。
16. 某企业职工的月工资数统计如下:
某企业职工的月工资数统计如下:
|
月工资数(元) |
10000 |
8000 |
5500 |
2500 |
1600 |
1200 |
900 |
600 |
500 |
|
得此工资人数 |
1 |
3 |
3 |
8 |
20 |
35 |
45 |
3 |
2 |
经计算,该企业职工工资的平均值为1565元,中位数是_____元,众数是_______元;
 如何选取该企业的月工资代表数呢?企业法人主张用平均值,职工代表主张用众数,监管部门主张用中位数;
如何选取该企业的月工资代表数呢?企业法人主张用平均值,职工代表主张用众数,监管部门主张用中位数;
请你站在其中一立场说明理由:______________________________________________。
15. 已知
已知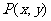 满足约束条件
满足约束条件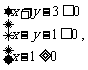 则
则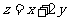 的最大值是________________;
的最大值是________________;
13.已知椭圆的中心在原点,焦点在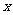 轴上,离心率为
轴上,离心率为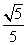 ,且过
,且过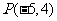 ,则椭圆的方程为________;
,则椭圆的方程为________;
12. 设函数
设函数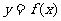 满足
满足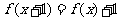 ,则函数
,则函数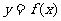 与
与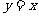 图象交点的个数可能是 ( )
图象交点的个数可能是 ( )
A.无穷多个 B.0个或者有限个 C.有限个 D.0个或者无穷多个
第Ⅱ卷(满分90分)
11. 已知
已知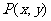 是函数
是函数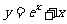 的图象上的点,则点
的图象上的点,则点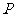 到直线
到直线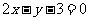 的最小距离为 ( )
的最小距离为 ( )
A.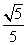 B.
B.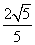 C.
C.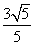 D.
D.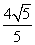
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com