
1.某商场有四类食品,其中粮食类、植物油类、动物性食品类及果蔬类分别有40种、10种、30种、20种,现从中抽取一个容量为20的样本进行食品安全检测。若采用分层抽样的方法抽取样本,则抽取的植物油类与果蔬类食品种数之和是 ( )
A.4 B.5 C.6 D.7
24.选修4-5:不等式选讲
设函数f(x)=|2x-1|+x+3,
(1)作出函数y=f(x)的图像并求函数y=f(x)的最小值;
(2)解不等式f(x)≤5。
23.选修4-4:坐标系与参数方程
设方程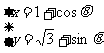 ,(θ为参数).表示的曲线为C,
,(θ为参数).表示的曲线为C,
(1)求曲线C上的动点到原点O的距离的最小值;
(2)点P为曲线C上的动点,当|OP|最小时(O为坐标原点),写出OP的参数方程并用直线参数方程求出点P的坐标。
22.选修4-1:几何证明选讲
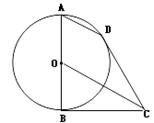
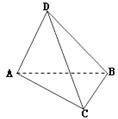
如图所示,AB为⊙O的直径,BC、CD为⊙O的切线,B、D为切点
(1)求证:AD∥OC;
(2)若⊙O的半径为1,求AD·OC的值。
21.(本小题满分12分)
已知函数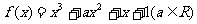
(1)讨论函数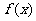 的单调区间;
的单调区间;
(2)设函数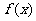 在区间
在区间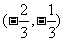 内是减函数,求
内是减函数,求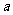 的取值范围。
的取值范围。
20.(本小题满分12分)
已知菱形ABCD的顶点A、C在椭圆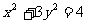 上对角线BD所在直线的斜率为1
上对角线BD所在直线的斜率为1
(1)当直线BD过点(0,1)时,求直线AC的方程;
(2)当∠ABC=60°时,求菱形ABCD面积的最大值.
19.(本小题满分12分)
如图,A、B、C、D为空间四点,在△ABC中,AB=2,AC=BC=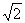 ,等边三角形ABD以AB为轴转动
,等边三角形ABD以AB为轴转动
(1)当面ABD⊥面ABC时,求CD长;
(2)当△ABD转动时,是否总有AB⊥CD?证明你的结论.
18.(本小题满分12分)
假设关于某设备的使用年限x和所支出的维修费用y(万元)有如下统计资料:
|
x |
2 |
3 |
4 |
5 |
6 |
|
y |
2.2 |
3.8 |
5.5 |
6.5 |
7.0 |
若由资料知y对x是线性相关关系,
试求:(1)线性回归方程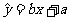 ;
;
(2)估计使用年限为10年时,维修费用是多少?
17.(本小题满分12分)
设数列{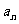 }的前
}的前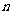 项和
项和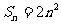 ,{
,{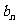 }为等比数列,且
}为等比数列,且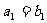 ,
,
(1)求数列{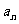 }和{
}和{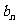 }的通项公式;
}的通项公式;
(2)设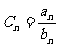 ,求数列{
,求数列{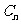 }的前
}的前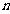 项和
项和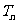 .
.
16.设F为椭圆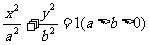 的一个焦点,已知长轴两个端点与F的距离为5和1,若点M(a,b),N(2,k)在直线y=kx的两侧,则k的取值范围__________________.
的一个焦点,已知长轴两个端点与F的距离为5和1,若点M(a,b),N(2,k)在直线y=kx的两侧,则k的取值范围__________________.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com