
5.设P为双曲线x2-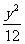 =1上的一点,F1、F2是双曲线的焦点,若|PF1|:|PF2|=3:2,则△PF1F2的面积为 ( )
=1上的一点,F1、F2是双曲线的焦点,若|PF1|:|PF2|=3:2,则△PF1F2的面积为 ( )
A.6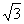 B.12 C.12
B.12 C.12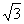 D.24
D.24
4.函数y=sin(2x+α)(0<α<π)的图象关于y轴对称,则函数y=cos(2x-α)是( )
A.奇函数 B.偶函数 C.既奇又偶 D.非奇非偶
3.圆2x2+2y2=1与直线xsinθ+y-1=0(θ≠kπ+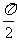 ,k∈Z)的位置关系是 ( )
,k∈Z)的位置关系是 ( )
A.相交 B.相切 C.相离 D.与θ有关
2.设函数f(x)定义在R上,它的图象关于直线x=1对称,且当x≥1时,f(x)=3x-1,则有 ( )
A.f(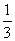 )<f(
)<f(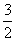 )<f(
)<f(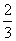 )
B.f(
)
B.f(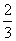 )<f(
)<f(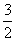 )<f(
)<f(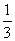 )
)
C.f(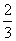 )<f(
)<f(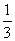 )<f(
)<f(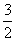 )
D.f(
)
D.f(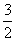 )<f(
)<f(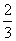 )<f(
)<f(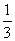 )
)
1.设全集U={1,3,5,7},M={1,|a-5|},M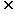 U,CUM={5,7},则a的值为 ( )
U,CUM={5,7},则a的值为 ( )
A.2或-8 B.-8或-2 C.-2或8 D.2或8
22.(本小题满分15分)
设函数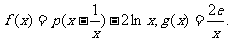 (p是实数,e是自然对数的底数)
(p是实数,e是自然对数的底数)
(1)若直线l与函数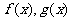 的图象都相切,且与函数
的图象都相切,且与函数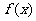 的图象相切于点(1,0),求p的值;
的图象相切于点(1,0),求p的值;
(2)若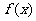 在其定义域内为单调函数,求p的取值范围;
在其定义域内为单调函数,求p的取值范围;
(3)若在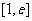 上至少存在一点
上至少存在一点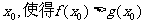 成立,求p的取值范围.
成立,求p的取值范围.
21.(本小题满分15分)
如图,椭圆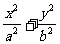 =1的两焦点F1,F2与短轴两端点B1,B2构成∠B2F1B1为120°,面积为
=1的两焦点F1,F2与短轴两端点B1,B2构成∠B2F1B1为120°,面积为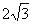 的菱形。
的菱形。
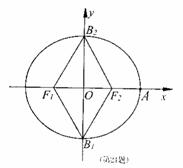
(1)求椭圆的方程;
(2)若直线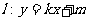 与椭圆相交于M,N两点(M,N不是左右顶点),且以MN为直径的圆过椭圆右顶点A,求证:直线l过定点,并求出该定点的坐标。
与椭圆相交于M,N两点(M,N不是左右顶点),且以MN为直径的圆过椭圆右顶点A,求证:直线l过定点,并求出该定点的坐标。
20.(本小题满分14分)
如图,一棱长为2的正四面体O-ABC的顶点O在平面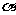 内,底面ABC平行于平面
内,底面ABC平行于平面 ,平面OBC与平面
,平面OBC与平面 的交线为l。
的交线为l。
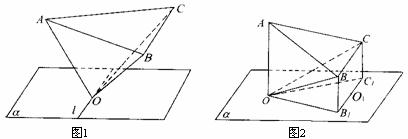
(1)当平面OBC绕l顺时针旋转与平面 第一次重合时,求平面OBC转过角的正弦值。
第一次重合时,求平面OBC转过角的正弦值。
(2)在上述旋转过程中,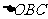 在平面
在平面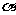 上的投影为等腰
上的投影为等腰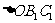 (如图1),B1C1的中点为O1。当AO⊥平面
(如图1),B1C1的中点为O1。当AO⊥平面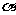 时,问在线段OA上是否存在一点P,使O1P⊥OBC?请说明理由。
时,问在线段OA上是否存在一点P,使O1P⊥OBC?请说明理由。
19.(本小题满分14分)
一个盒子中装有分别标有数字1,2,3,4的4个大小、形状完全相同的球,现从中有放回地随机抽取2个球,抽取的球的标号分别为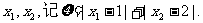
(1)求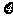 取得最大值时的概率;
取得最大值时的概率;
(2)求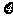 的分布列及数学期望.
的分布列及数学期望.
18.(本小题满分14分)
在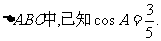
(1)求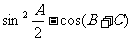 的值;
的值;
(2)若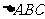 的面积为4,AB=2,求BC的长。
的面积为4,AB=2,求BC的长。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com