
21.(本小题满分13分)
已知函数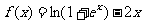 .点
.点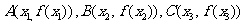 均在函数
均在函数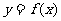 的图象上,且
的图象上,且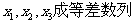 ,其公差为
,其公差为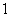 .
.
(1)判断函数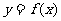 是否有极值,并说明理由;
是否有极值,并说明理由;
(2)求证:△ABC是钝角三角形;
(3)求△ABC面积的最大值.
20.(本小题满分13分)
已知F1、F2分别是椭圆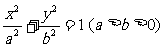 的左、右焦点,P是此椭圆上的一动点,并且
的左、右焦点,P是此椭圆上的一动点,并且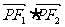 的取值范围是
的取值范围是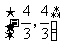
(1)求此椭圆的方程;
(2)点A是椭圆的右顶点,直线y = x与椭圆交于B、C两点(C在第一象限内),又P、Q是椭圆上两点,并且满足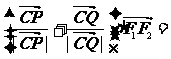 0,试问:向量
0,试问:向量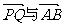 是否共线,并说明理由。
是否共线,并说明理由。
19.(本小题满分13分)
已知定义在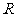 上的函数
上的函数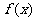 满足:对任意实数
满足:对任意实数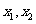 ,总有
,总有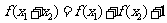
恒成立,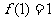 ,且对任意正整数
,且对任意正整数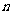 ,有
,有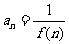 ,
,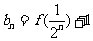 .
.
(1)求数列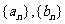 的通项公式;
的通项公式;
(2)记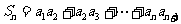 ,
,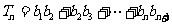 ,比较
,比较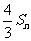 与
与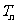 的大小关系,并给出证明;
的大小关系,并给出证明;
18.(本小题满分12分)
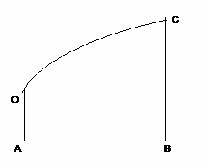
某地政府为科技兴市,欲将如图所示的一块不规则的非农业用地规划建成一个矩形高科技工业园区.已知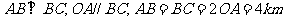 ,曲线段
,曲线段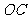 是以点
是以点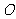 为顶点且开口向右的抛物线的一段.如果要使矩形的相邻两边分别落在
为顶点且开口向右的抛物线的一段.如果要使矩形的相邻两边分别落在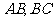 上,且一个顶点落在曲线段
上,且一个顶点落在曲线段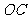 上,问应如何规划才能使矩形工业园区的用地面积最大?并求出最大的用地面积(精确到
上,问应如何规划才能使矩形工业园区的用地面积最大?并求出最大的用地面积(精确到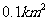 ).
).
17.(本小题满分12分)
如图,在四棱锥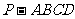 中,底面
中,底面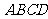 为正方形,且
为正方形,且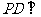 平面
平面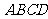 ,
,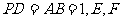 分别是
分别是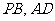 的中点.
的中点.
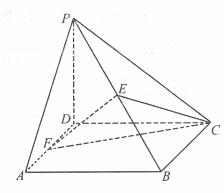
(1)证明: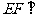 平面
平面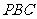 ;
;
(2)求二面角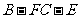 的大小.
的大小.
16.(本小题满分12分)
已知函数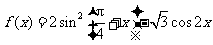
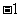 ,
,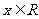 .
.
(1)求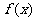 的最值和最小正周期;
的最值和最小正周期;
(2)设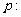
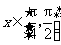 ,
,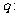
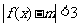 ,若
,若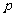 是
是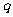 的充分条件,求实数
的充分条件,求实数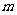 的取值范围.
的取值范围.
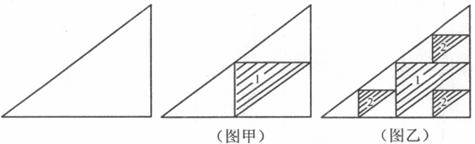
15.如下图,对一个边长分别为3、4、5的直角三角形进行如下操作:第一次操作,分别连接这个三角形三边的中点,构成4个小三角形,挖去中间一个阴影部分三角形(如图甲);第二次操作,分别连接剩余的三个三角形三边的中点,再挖去各自中间的阴影部分三角形(如图乙);第三次操作,分别连接剩余的各个三角形的中点,再挖去各自中间阴影部分的三角形;……;如此操作下去,记第 次操作后剩余图形的面积总和为
次操作后剩余图形的面积总和为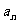 .
.
(i)则数列{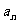 }的通项公式
}的通项公式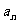 =_______.(ii)如图乙,把第一次操作挖去的阴影部分三角形贴上数字标签“1”,第二次操作挖去的每个阴影部分三角形都贴上数字标签“2”,第三次操作挖去的每个阴影部分三角形都贴上数字标签“3”,……,第
=_______.(ii)如图乙,把第一次操作挖去的阴影部分三角形贴上数字标签“1”,第二次操作挖去的每个阴影部分三角形都贴上数字标签“2”,第三次操作挖去的每个阴影部分三角形都贴上数字标签“3”,……,第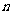 次操作挖去的每个阴影部分三角形都贴上数字标签“
次操作挖去的每个阴影部分三角形都贴上数字标签“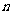 ”,则第
”,则第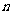 次操作后,所有标签的数字之和
次操作后,所有标签的数字之和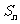 =_______.
=_______.
14.已知定义在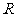 上的单调函数
上的单调函数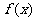 满足:存在实数
满足:存在实数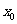 ,使得对于任意实数
,使得对于任意实数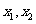 ,总有
,总有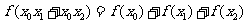 恒成立,则(i)
恒成立,则(i)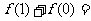 _______;(ii)
_______;(ii)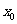 的值为_______;
的值为_______;
13.已知体积为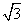 的正三棱锥
的正三棱锥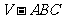 的外接球的球心为O,满足
的外接球的球心为O,满足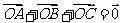 ,则三棱锥外接球的体积为_______.
,则三棱锥外接球的体积为_______.
12.设 在R内每一点处都连续,那么a=_______.
在R内每一点处都连续,那么a=_______.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com