
8.已知长方形的四个顶点A(0,0),B(2,0),C(2,1)和D(0,1).一质点从AB的中点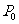 沿与AB夹角为θ的方向射到BC上的点
沿与AB夹角为θ的方向射到BC上的点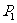 后,依次反射到CD、DA和AB上的点
后,依次反射到CD、DA和AB上的点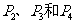 (入射角等于反射角).设
(入射角等于反射角).设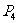 的坐标为
的坐标为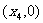 ,若
,若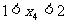 则tanθ的取值范围是
则tanθ的取值范围是
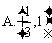
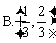
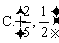
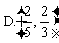
7.已知某正项等差数列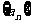 ,若存在常数
,若存在常数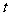 ,使得
,使得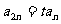 对一切
对一切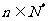 成立,则
成立,则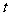 的集合是
的集合是
A.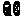 B.
B.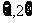 C.
C.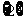 D.
D.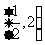
6.某外商计划在5个候选城市投资3个不同的项目,且在同一个城市投资的项目不超过2个,则该外商不同的投资方案有
A.60种 B.70种 C.80种 D.120种
5.如图S为正三角形ABC所在平面外一点,且SA=SB=SC=AB,E、F分别为SC、AB中点,则异面直线EF与SA所成角为
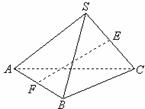
A.90º B.60º C.45º D.30º
4.函数f(x)=sin2x+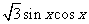 在区间
在区间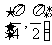 上的最大值是
上的最大值是
A.1 B.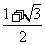 C.
C.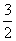 D.1+
D.1+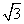
3.已知映射f:A→B,其中A=B=R,对应法则f:x→y=x2-2x+2.若对实数k∈B,在集合A中不存在原象,则k的取值范围是
A.k≤1 B.k<1 C.k≥1 D.k>1
2.下列命题中,m,n表示两条不同的直线,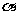 、
、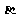 、
、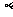 表示三个不同的平面.
表示三个不同的平面.
①若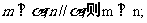 ②若
②若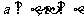 ,则
,则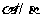 ;③若
;③若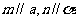 ,则
,则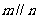 ;④若
;④若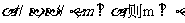 .正确的命题是
.正确的命题是
A.①③ B.②③ C.①④ D.②④
1.已知向量a、b的夹角为60°且|a|=2,|b|=3,则a2+a·b=
A.7 B.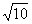 C.10 D.49
C.10 D.49
21.(本小题满分13分) 已知定义在R上的函数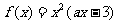 ,其中a为常数.
,其中a为常数.
(1)若函数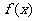 在区间(-1,0)上是增函数,求a的取值范围;
在区间(-1,0)上是增函数,求a的取值范围;
(2)若函数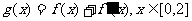 ,在x=0处取得最大值,求正数a的取值范围.
,在x=0处取得最大值,求正数a的取值范围.
20.(本小题满分13分)已知双曲线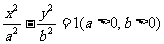 的一条渐近线方程为
的一条渐近线方程为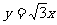 两条准线间的距离为1.
两条准线间的距离为1.
(1)求双曲线的方程;
(2)直线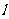 过坐标原点
过坐标原点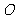 且和双曲线交于两点M、N,点P为双曲线上异于M、N的一点,且直线PM、PN的斜率均存在,求kPM·kPN的值.
且和双曲线交于两点M、N,点P为双曲线上异于M、N的一点,且直线PM、PN的斜率均存在,求kPM·kPN的值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com