
7.已知函数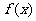 满足
满足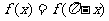 ,且当
,且当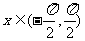 时,
时,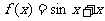 ,
,
设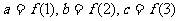 ,则
,则
A.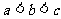 B.
B.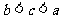 C.
C. 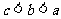 D.
D.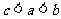
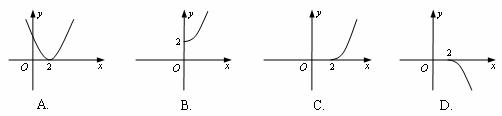
6.设函数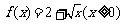 ,则其反函数
,则其反函数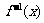 的图象是
的图象是
5.若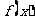 是R上的增函数,且
是R上的增函数,且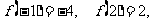 设P=
设P= ,
,
Q=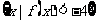 .若“
.若“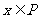 ”是“
”是“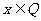 ”的充分不必要条件,则实数t的取值范围是
”的充分不必要条件,则实数t的取值范围是
A.t≤-1 B.t>-1 C.t≥3 D.t>3
4.定义集合M与N的新运算:M+N=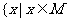 或
或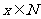 且
且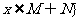 ,则(M+N)+N等于
,则(M+N)+N等于
A.M B.N
C.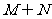 D.
D.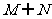
3.在等比数列{an}中,若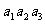 = 2 ,
= 2 , 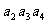 = 16,则公比q =
= 16,则公比q =
A.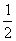 B.2 C.
B.2 C.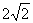 D.8
D.8
2.设集合S = {0 , 1 , 2 , 3 } , T = { x | | x –3 | ≤2},则S∩T =
A.{0 , 1, 2 , 3 } B.{1 , 2 , 3 } C.{0 ,1 } D.{1}
1.若复数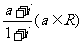 是纯虚数,则实数
是纯虚数,则实数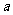 的值为
的值为
A.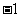 B.
B.
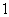 C.
C. D.
D.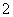
(17)(本小题满分10分)
设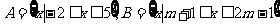 若
若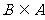 ,求实数
,求实数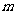 的取值范围。
的取值范围。
(18)(本小题满分12分)
已知数列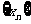 的首项
的首项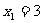 ,通项
,通项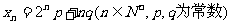 ,且
,且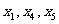 成等差数列.
成等差数列.
求: (1)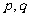 的值; (2)数列
的值; (2)数列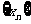 前
前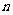 项和
项和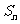 的公式.
的公式.
(19)(本小题满分12分)
已知函数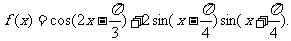
(1)求函数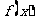 的最小正周期;
的最小正周期;
(2)求函数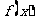 在区间
在区间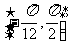 上的值域.
上的值域.
(20)(本小题满分12分)
已知函数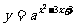 ,当
,当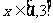 时,该函数有最小值8,求
时,该函数有最小值8,求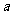 的值。
的值。
(21)(本小题满分12分)
已知函数 的图象过点(-1,-6),且函数
的图象过点(-1,-6),且函数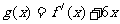 的图象关于
的图象关于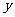 轴对称.
轴对称.
(1)求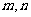 的值及函数
的值及函数 的单调区间;
的单调区间;
(2)求函数 在区间
在区间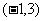 内的极值.
内的极值.
(22)(本小题满分12分)
设函数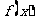 对于任意
对于任意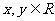 ,都有
,都有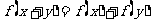 ,
,
且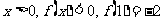
(1)求证: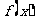 是奇函数,
是奇函数,
(2)试问在 时,
时,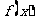 是否有最值?如果有,求出最值;如果没有,说出理由。
是否有最值?如果有,求出最值;如果没有,说出理由。
(13)函数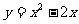 在区间
在区间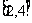 上的最小值是
上的最小值是
(14)函数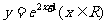 的反函数是
.
的反函数是
.
(15)某校有老师200人,男生学1200人,女学生1000人。现用分层抽样的方法从所有师生中抽取一个容量为n的样本;已知从女学生中抽取的人数为80人,则n= .
(16)已知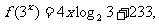 ,则
,则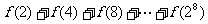 的值等于____________.
的值等于____________.
(1)已知集合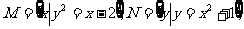 那么
那么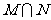 等于: ( )
等于: ( )
A.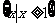 B.
B.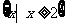
C.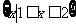 D.R
D.R
(2)下列各组中两个函数是同一个函数的对数为: ( )
①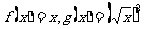 ;
②
;
②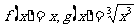 ;
;
③ ; ④
; ④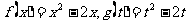 .
.
A.0对 B.一对 C.两对 D.三对
(3)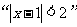 是“
是“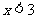 ”的
( )
”的
( )
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分也不必要条件
(4)把函数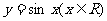 的图象上所有的点向左平行移动
的图象上所有的点向左平行移动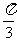 个单位长度,再把所得图象上所有点的横坐标缩短到原来的
个单位长度,再把所得图象上所有点的横坐标缩短到原来的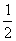 倍(纵坐标不变),得到的图象所表示的函数是 ( )
倍(纵坐标不变),得到的图象所表示的函数是 ( )
A.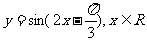 B.
B.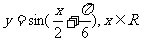
C.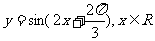 D.
D.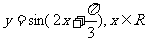
(5)函数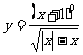 的定义域是:( )
的定义域是:( )
A.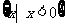 B.
B.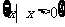
C.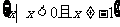 D.
D.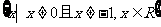
(6)已知等差数列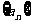 中,
中,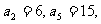 若
若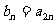 ,则数列
,则数列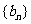 的前5项和等于( )
的前5项和等于( )
A.30 B.45 C.90 D.186
(7)已知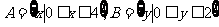 ,下列对应不表示从
,下列对应不表示从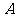 到
到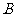 的映射的是( )
的映射的是( )
A.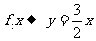 B.
B.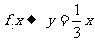
C.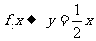 D.
D.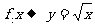
(8)当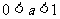 时,在同一坐标系中,函数
时,在同一坐标系中,函数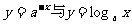 的图象是( )
的图象是( )
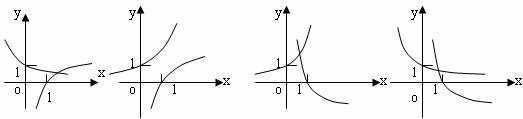
A B C D
(9)如函数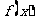 是定义在
是定义在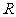 上的偶函数,在
上的偶函数,在  上是减函数,且
上是减函数,且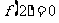 ,则使得
,则使得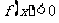 的
的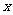 的取值范围是:
( )
的取值范围是:
( )
A. B.
B.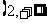
C.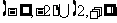 D.
D.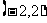
(10)若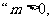 则
则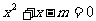 有实数根”为原命题,则原命题与其逆命题、否命题、逆否命题这四个命题中,假命题的个数是( )
有实数根”为原命题,则原命题与其逆命题、否命题、逆否命题这四个命题中,假命题的个数是( )
A. 0 B. 1 C. 2 D. 3
(11)设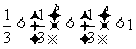 ,则: ( )
,则: ( )
A.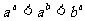 B.
B. 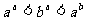
C.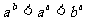 D.
D.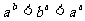
(12) 给出下列结论;
①当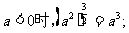
②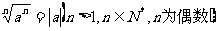
③函数
④若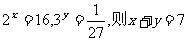
其中正确的是:( )
A.① ② B.② ③
C.③ ④ D.② ④
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com