
5.已知函数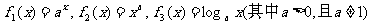 在同一坐标系中画出其中两个函数在第一象限内的图象,其中正确的是
在同一坐标系中画出其中两个函数在第一象限内的图象,其中正确的是
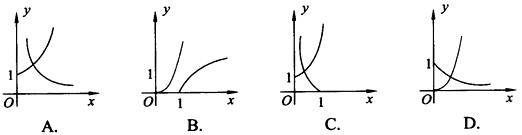
4.下表是某厂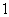 -4月份用水量(单位:百吨)的一组数据:
-4月份用水量(单位:百吨)的一组数据:
月份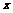 |
1 |
2 |
3 |
4 |
用水量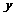 |
4.5 |
4 |
3 |
2.5 |
由散点图可知,用水量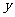 与月份
与月份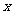 之间有较好的线性相关关系,其线性回归直线方程是
之间有较好的线性相关关系,其线性回归直线方程是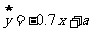 ,则
,则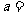
A.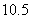 B.
B. 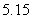 C.
C.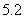 D.
D.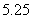
3.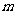 、
、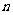 是不同的直线,
是不同的直线,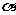 、
、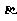 、
、 是不同的平面,有以下四个命题:
是不同的平面,有以下四个命题:
① 若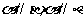 ,则
,则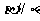 ; 若
; 若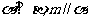 ,则
,则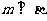 ;
;
③ 若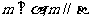 ,则
,则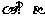 ; 若
; 若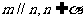 ,则
,则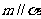 .
.
其中真命题的序号是
A.①③ B.①④ C.②③ D.②④
2.函数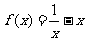 的图像关于
的图像关于
A.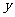 轴对称 B.直线
轴对称 B.直线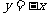 对称
对称
C.坐标原点对称 D.直线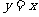 对称
对称
1.定义集合运算: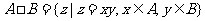 ,设
,设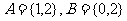 ,则集合
,则集合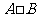 的真子集个数为
的真子集个数为
A.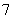 B.
B.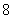 C.
C.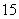 D.
D.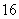
24.(本小题满分10分)选修4-5;不等式选讲.
对于任意的实数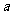 (
(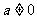 )和
)和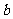 ,不等式
,不等式 恒成立,记实数
恒成立,记实数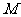 的最大值是
的最大值是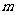 .
.
(Ⅰ)求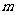 的值;
的值;
(Ⅱ)解不等式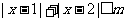 .
.
23.(本小题满分10分)选修4-4:坐标系与参数方程.
已知曲线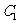 :
: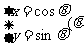 为参数),曲线
为参数),曲线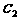 :
: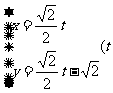 为参数)
为参数)
(Ⅰ)曲线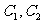 是否有公共点, 为什么?
是否有公共点, 为什么?
(Ⅱ)若把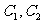 上各点的横坐标都压缩为原来的一半,分别得到曲线
上各点的横坐标都压缩为原来的一半,分别得到曲线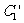 ,
,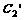 .问
.问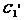 与
与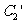 公共点的个数和
公共点的个数和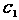 与
与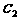 公共点的个数是否相同?说明你的理由.
公共点的个数是否相同?说明你的理由.
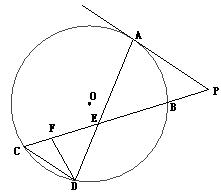
22.(本小题满分10分)选修4-1:几何证明选讲.
如图所示,已知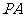 与⊙
与⊙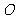 相切,
相切,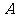 为切点,
为切点,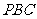 为割线,弦
为割线,弦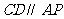 ,
,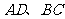 相交于
相交于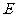 点,
点,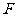 为
为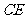 上一点,且
上一点,且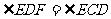 .
.
(Ⅰ)求证: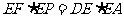 ;
;
(Ⅱ)若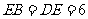 ,
,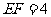 ,求
,求 的长.
的长.
21.(本小题满分12分)
已知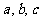 是不全为0的实数,函数
是不全为0的实数,函数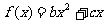 ,方程
,方程
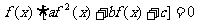 恰有两个不同的实数根.
恰有两个不同的实数根.
(Ⅰ)若a=0,b≠0,求c的取值范围;
(Ⅱ)若a=1,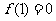 ,求正实数c的取值范围.
,求正实数c的取值范围.
选考题:请考生在第22、23、24题中任选一题做答,如果多做,则按所做的第一题记分.做答时用2B铅笔在答题卡上把所选题目对应的题号涂黑.
20.(本小题满分12分)
设点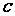 为曲线
为曲线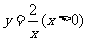 上任一点,以点
上任一点,以点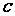 为圆心的圆与
为圆心的圆与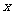 轴交于点
轴交于点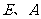 ,与轴交于点
,与轴交于点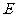 、
、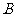 .
.
(1)证明:多边形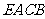 的面积是定值,并求这个定值;
的面积是定值,并求这个定值;
(2)设直线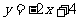 与圆
与圆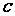 交于点
交于点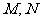 ,若
,若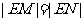 ,求圆
,求圆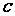 的方程.
的方程.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com