
19.(本小题满分12分)( 请同学们注意:此题求证方法只能应用几何法推证,不能使用坐标解析法,否则不得分. )
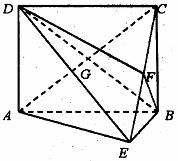
如图,矩形ABCD中,AD⊥平面ABE,AE=EB=BC=2,F为CE上的点,且BF⊥平面ACE,AC∩BD=G.
(1)求证:AE⊥平面BCE;
(2)求证:AE//平面BFD;
(3)求三棱锥C-BGF的体积.
18.(本小题满分12分)
某种汽车的购车费用是10万元,每年使用的保险费、养路费、汽油费约为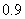 万元,年维修费用第一年是
万元,年维修费用第一年是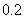 万元,以后逐年递增
万元,以后逐年递增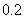 万元。问这种汽车使用多少年时,它的年平均费用最小?最小值是多少?
万元。问这种汽车使用多少年时,它的年平均费用最小?最小值是多少?
17.(本小题满分12分)
已知函数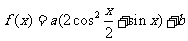 .
.
(Ⅰ)当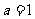 时,求函数
时,求函数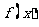 的单调递增区间;.
的单调递增区间;.
(Ⅱ)当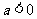 时,若
时,若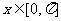 ,函数
,函数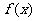 的值域是
的值域是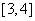 ,求实数
,求实数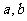 的值。
的值。
16.给出下列命题:
①函数f(x)=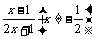 对称中心是(-
对称中心是(-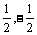 );
);
②已知Sn是等差数列{an}(n∈N*)的前n项和,若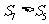 ,则
,则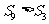 ;
;
③函数f(x)=x|x|+px+q(x∈R)为奇函数的充要条件是q=0;
④已知a,b,m均是正数,且a<b,则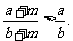
其中真命题的序号是_______(将所有真命题的序号都填上).
15.已知向量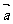 、
、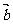 的夹角为60°,且
的夹角为60°,且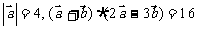 ,则
,则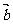 在
在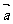 方向上的投影等于 .
方向上的投影等于 .
14.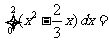 .
.
13.不论m取何值时,直线(m-1)x-y+2m+1=0恒过定点 .
12.若直线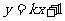 与圆
与圆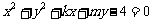 交于
交于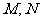 两点,且
两点,且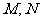 关于直线
关于直线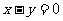 对称, 动点P
对称, 动点P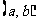 在不等式组
在不等式组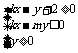 表示的平面区域内部及边界上运动,则
表示的平面区域内部及边界上运动,则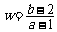 的取值范围是 ( )
的取值范围是 ( )
A.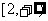 B.
B. C.
C.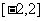 D.
D.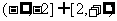
11.设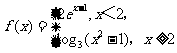 ,则不等式f(x)>2的解集为 ( )
,则不等式f(x)>2的解集为 ( )
A.(1,2)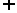 (3,+∞) B.(
(3,+∞) B.(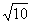 ,+∞)
,+∞)
C.(1,2)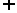 (
(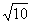 ,+∞) D.(1,2)
,+∞) D.(1,2)
10.给出下列命题:①若平面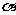 内的直线
内的直线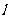 垂直于平面
垂直于平面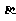 内的任意直线,则
内的任意直线,则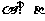 ;②若平面
;②若平面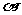 内的任一直线都平行于平面
内的任一直线都平行于平面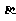 ,则
,则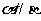 ;③底面是等边三角形,侧面都是等腰三角形的三棱锥是正三棱锥;④若两个过相对侧棱的截面都垂直于底面,则该四棱柱为直四棱柱.其中为假命题的个数 ( )
;③底面是等边三角形,侧面都是等腰三角形的三棱锥是正三棱锥;④若两个过相对侧棱的截面都垂直于底面,则该四棱柱为直四棱柱.其中为假命题的个数 ( )
A.1 B.2 C.3 D.4
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com