
21.(12分)已知数列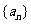 中,
中,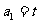 ,
,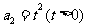 且
且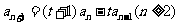 。
。
(1)若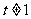 ,求证:数列
,求证:数列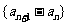 是等比数列;
是等比数列;
(2)求数列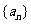 的通项公式;
的通项公式;
(3)若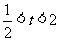 ,
,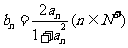 ,试比较
,试比较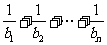 与
与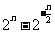 大小。
大小。
20.(12分)已知函数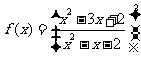 ,其中
,其中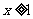 且
且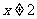
(1)求函数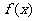 的反函数
的反函数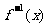 ;
;
(2)设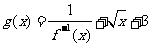 ,求函数
,求函数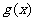 的最小值及相应的
的最小值及相应的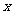 的值;
的值;
(3)若不等式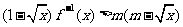 对于区间
对于区间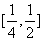 上的每一个
上的每一个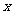 值都成立,求实数
值都成立,求实数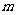 的取值范围。
的取值范围。
19.(12分)已知数列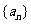 的前
的前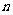 项和为
项和为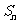 ,且对任意
,且对任意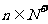 ,有
,有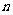 ,
,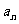 ,
,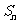 成等差数列。
成等差数列。
(1)求数列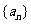 的通项公式;
的通项公式;
(2)求数列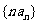 的前
的前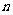 项和
项和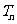 。
。
18.(12分)已知函数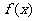 的图象与
的图象与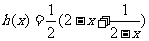 的图象关于直线
的图象关于直线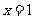 对称,函数
对称,函数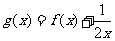
(1)判断函数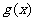 的奇偶性;
的奇偶性;
(2)求函数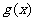 在区间
在区间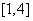 上的最大值和最小值。
上的最大值和最小值。
17.(12分)函数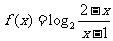 的定义域为集合
的定义域为集合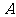 ,关于
,关于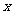 的不等式
的不等式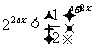
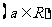 的解集为
的解集为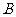 ,求使
,求使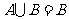 的实数
的实数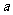 的取值范围。
的取值范围。
16.若函数 在
在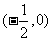 内单调递增,则实数
内单调递增,则实数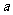 的取值范围是___________________。
的取值范围是___________________。
15.已知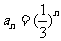 ,把数列
,把数列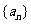 的各项排成如图的三角形形状,记
的各项排成如图的三角形形状,记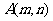 表示第
表示第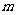 行,第
行,第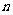 列的项,则
列的项,则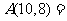 _____________,
_____________,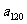 在图中的位置是_________________。
在图中的位置是_________________。
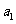
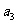
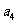
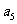
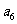
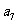
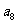
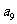
……………………….
14.在数列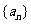 中,
中,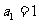 ,
,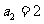 ,且
,且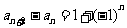 ,则
,则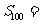 _____________。
_____________。
13.设命题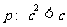 和命题
和命题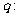 对任意
对任意 恒成立,且
恒成立,且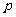 或
或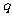 为真,
为真,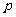 且
且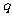 为假. 则实数
为假. 则实数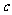 的取值范围是___________________。
的取值范围是___________________。
12.若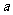 是
是 与
与 的等比中项,则
的等比中项,则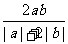 的最大值为
的最大值为
A.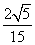 B.
B.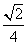 C.
C.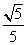 D.
D.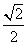
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com