21．(本小题满分14分)

　　 已知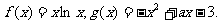

　 (I)求函数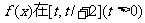上的最小值；

　 　(II)对一切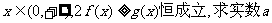的取值范围；

20．(本小题满分12分)

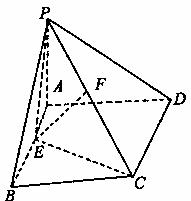
　　　　 如图，四棱锥P-ABCD，底面ABCD是矩形，PA⊥平面ABCD，PA=AD，点E、F分别是AB、PC的中点。

　 (I)求证：EF//平面PAD；

　 (II)求证：平面PEC⊥平面PCD。

19．(本小题满分12分)

　　 已知⊙O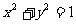：和定义A(2，1)，由⊙O外一点P(a，b)向⊙O引切线PQ，切点Q，且满足|PQ|=|PA|。

　 (1)求实数a、b间满足的等量关系；

　 (2)求线段PQ长的最小值；

　 (3)若以P为圆心所作的⊙P与⊙Q有公共点，试求半径取最小值时，⊙P的方程。

18．(本小题满分12分)

　　　　 某观测站C在城A的南偏西20°的方向上，由A城出发有一条公路，走向是南偏东40°，在C处测得距C为31千米的公路上B处有一人正沿公路向A城走去，走了20千米后，到达D处，此时C、D间距离为21千米，问这人还需要走多少千米到达A城？

17．(本小题满分12分)

　　 已知向量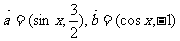

　 (I)当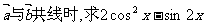的值；

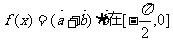　 (II)求上的值域。

16．已知定义在R上的偶函数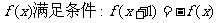，且在[-1，0]上是增函数，给出下面关于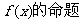：①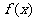是周期函数；②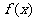的图象关于直线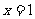对称；③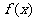在[0，1]上是增函数；④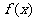在[1，2]上是减函数；⑤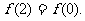其中正确的命题序号是　　　　 。(注：把你认为正确的命题序号都填上)

15．设O是△ABC内部一点，且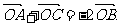则△AOB与△AOC面积之比是　　　 。

14．若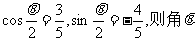的终边所在直线方程为　　　　 。

13．设集合=　　　　 。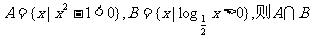

12．某公司有60万元资金，计划投资甲、乙两个项目，按要求对项目甲的投资不小于对项目乙投资的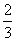倍，且对每个项目的投资不能低于5万元，对项目甲每投资1万元可获得0.4万元的利润，对项目乙每投资1万元可获得0.6万元的利润，该公司正确规划投资后，在这两个项目上共可获得的最大利润为　　　　　　　　　　　　　　 (　　 )

　　　 A．36万元　　　　　　　 B．31.2万元　　　　　　 C．30.4万元　　　　　　 D．24万元