
21.(本小题满分12分)
已知椭圆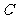 的中心在坐标原点,焦点在
的中心在坐标原点,焦点在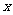 轴上,椭圆
轴上,椭圆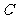 上的点到焦点距离的最大值为
上的点到焦点距离的最大值为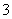 ,最小值为
,最小值为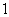 。
。
(1)求椭圆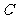 的标准方程;
的标准方程;
(2)若直线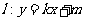 与椭圆
与椭圆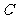 相交于
相交于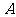 ,
,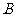 两点(
两点(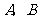 不是左,右顶点),且以
不是左,右顶点),且以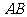 为直径的圆过椭圆
为直径的圆过椭圆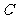 的右顶点,求证:直线
的右顶点,求证:直线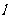 过定点,并求出该定点的坐标。
过定点,并求出该定点的坐标。
20.(本小题满分12分)
已知数列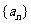 的前
的前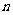 项和为
项和为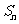 ,且有
,且有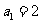 ,
,
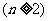 。
。
(1)求数列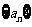 的通项公式
的通项公式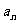 ;
;
(2)若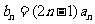 ,求数列
,求数列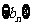 的前
的前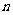 项和
项和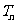 。
。
19.(本小题满分12分)
如下图,在直三棱柱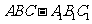 中,平面
中,平面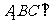 侧面
侧面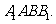
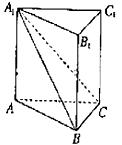
(1)求证: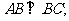
(2)若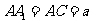 ,直线
,直线 与平面
与平面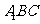 所成的角为
所成的角为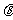 ,二面角
,二面角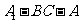 的大小为
的大小为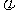 ,求
,求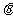
 的值。
的值。
18.(本小题满分12分)
甲、乙、丙三人按下面的规则进行乒乓球比赛:第一局由甲、乙参加而丙轮空,以后每一局由前一局的获胜者与轮空者进行比赛,而前一局的失败者轮空。比赛按这种规则一直进行到其中一人连胜两局或打满6局时停止。设在每局中参赛者胜负的概率均为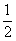 ,且各局胜负相互独立。求:
,且各局胜负相互独立。求:
(1)打满3局比赛还未停止的概率;
(2)比赛停止时已打局数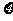 的分别列与期望E
的分别列与期望E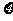 。
。
17.(本小题满分10分)
已知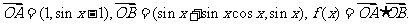 (
(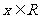 )
) 求:
求:
(1)函数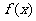 的最大值和相应的
的最大值和相应的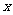 的取值的集合。
的取值的集合。
(2)函数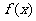 的单调递增区间。
的单调递增区间。
16.已知函数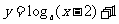
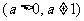 的图象恒过定点A,若点A在直线
的图象恒过定点A,若点A在直线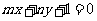 上,其中
上,其中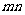 >0,则
>0,则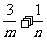 的最大值为 。
的最大值为 。
15.将7个不同的小球全部放入编号为2和3的两个盒子里,使得放入每个盒子里的球的个数不少于该盒子的编号,则不同的放球方法共有________种(用数字作答)。
14.在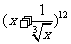 的展开式中的常数项是_____________。
的展开式中的常数项是_____________。
13.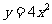 的焦点到准线的距离为
。
的焦点到准线的距离为
。
12.定义在 上的可导函数
上的可导函数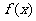 满足
满足 且
且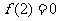 ,则
,则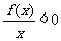 的解集为
的解集为
A.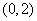 B.
B.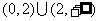 C.
C. D.
D.
第Ⅱ卷(非选择题,共90分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com