
7.将函数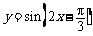 的图象先向左平移
的图象先向左平移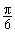 ,然后将所得图象上所有点的横坐标变为原来的2倍(纵坐标不变),则所得到的图象对应的函数解析式为 .
,然后将所得图象上所有点的横坐标变为原来的2倍(纵坐标不变),则所得到的图象对应的函数解析式为 .
5.已知复数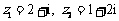 ,则
,则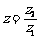 在复平面内所对应的点位于第 象限.
在复平面内所对应的点位于第 象限.
6已知向量a=(1,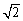 ),b=(
),b=(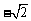 ,1),若正数k和t,使得x=a+(t2+1)b与y=-ka+
,1),若正数k和t,使得x=a+(t2+1)b与y=-ka+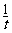 b垂直,则k的最小值是 .
b垂直,则k的最小值是 .
4.计算机的价格大约每3年下降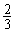 ,那么今年花8100元买的一台计算机,9年后的价格大约是 元.
,那么今年花8100元买的一台计算机,9年后的价格大约是 元.
3.在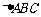 中,
中,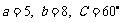 , 则
, 则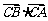 的值为 .
的值为 .
2.已知集合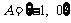 ,集合
,集合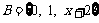 , 且
, 且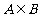 ,则实数x的值为 .
,则实数x的值为 .
1.命题“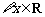 ,
,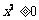 ”的否定是 .
”的否定是 .
22.(本小题满分12分)
如图,把正 分成有限个全等的小正三角形,且在每个小三角形的顶点上都放置一个非零实数,使得任意两个相邻的小三角形组成的菱形的两组相对顶点上实数的乘积相等.设点A为第一行,...,BC为第n行,记点A上的数为
分成有限个全等的小正三角形,且在每个小三角形的顶点上都放置一个非零实数,使得任意两个相邻的小三角形组成的菱形的两组相对顶点上实数的乘积相等.设点A为第一行,...,BC为第n行,记点A上的数为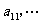 ,第i行中第j个数为
,第i行中第j个数为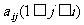 .若
.若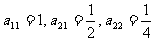 .
.
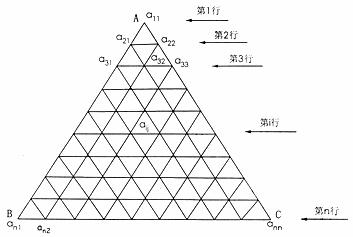
(1)求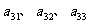 ;
;
(2)试求第n行中第m个数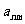 的表达式(用n、m表示);
的表达式(用n、m表示);
(3)记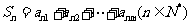 ,求证:
,求证: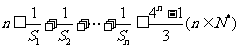
21.(本小题满分12分)
若函数 为奇函数,且过点
为奇函数,且过点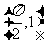 ,函数
,函数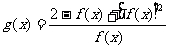 .
.
(1)求函数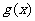 的解析式并求其定义域;
的解析式并求其定义域;
(2)求函数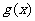 的单调区间;
的单调区间;
(3)若当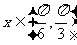 时不等式
时不等式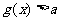 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.
20.(本小题满分12分)
已知数列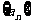 的前n项和为Sn,且
的前n项和为Sn,且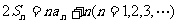 ,等比数列
,等比数列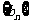 中
中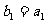 ,且
,且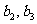 的等差中项为
的等差中项为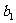 .
.
(1)求证:数列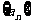 为等差数列;
为等差数列;
(2)请选择一个符合已知条件的且满足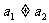 的数列
的数列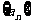 ,并求数列
,并求数列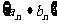 的前n项和Tn.
的前n项和Tn.
19.(本小题满分12分)
袋中有3个白球,2个红球和若干个黑球(球的大小均相同),从中任取2个球,设每取得一个黑球得0分,每取得一个白球得1分,每取得一个红球得2分,已知得0分的概率为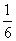 .
.
(1)求袋中黑球的个数及得2分的概率;
(2)设所得分数为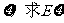 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com