
22.(本小题满分10分)选修4-1:几何证明选讲
如下图,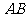 是⊙
是⊙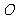 的直径,
的直径,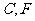 是⊙
是⊙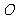 上的点,
上的点,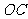 垂直于直径
垂直于直径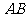 ,过
,过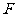 点作⊙
点作⊙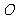 的切线交
的切线交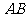 的延长线于
的延长线于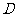 .连结
.连结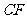 交
交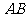 于
于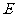 点.
点.
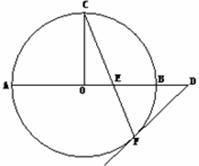
(Ⅰ)求证: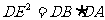 ;
;
(Ⅱ)若⊙ 的半径为
的半径为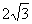 ,
,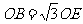 ,求
,求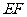 的长.
的长.
21.(本小题满分12分)
已知圆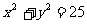 ,
,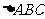 内接于此圆,
内接于此圆,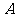 点的坐标
点的坐标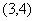 ,
,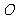 为坐标原点.
为坐标原点.
(Ⅰ)若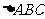 的重心是
的重心是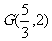 ,求直线
,求直线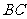 的方程;(三角形重心是三角形三条中线的交点,并且重心到顶点的距离是它到对边中点距离的两倍)
的方程;(三角形重心是三角形三条中线的交点,并且重心到顶点的距离是它到对边中点距离的两倍)
(Ⅱ)若直线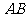 与直线
与直线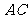 的倾斜角互补,求证:直线
的倾斜角互补,求证:直线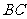 的斜率为定值.
的斜率为定值.
选考题:请考生在第22、23、24题中任选一题作答,如果多做,则按所做的第一题记分.作答时,用2B铅笔在答题卡上把所选题目对应的标号涂黑.
20.(本小题满分12分)
某班50名学生在一次百米测试中,成绩全部介于13秒与18秒之间,将测试结果按如下方式分成五组:每一组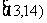 ;第二组
;第二组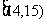 ……第五组
……第五组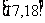 .下图是按上述分组方法得到的频率分布直方图.
.下图是按上述分组方法得到的频率分布直方图.
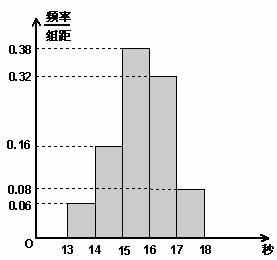
(I)若成绩大于或等于14秒且小于16秒认为良好,求该班在这次百米测试中成绩良好的人数;
(II)设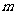 、
、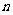 表示该班某两位同学的百米测试成绩,且已知
表示该班某两位同学的百米测试成绩,且已知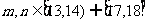 .求事件“
.求事件“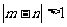 ”的概率.
”的概率.
19.(本小题满分12分)
设数列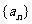 满足当
满足当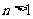 时,
时,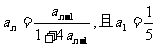 .
.
(Ⅰ)求证:数列 为等差数列;
为等差数列;
(Ⅱ)试问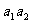 是否是数列
是否是数列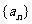 中的项?如果是,是第几项;如果不是,说明理由.
中的项?如果是,是第几项;如果不是,说明理由.
18.(本小题满分12分)
如下图,三棱柱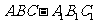 的所有棱长都相等,且
的所有棱长都相等,且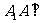 底面
底面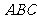 ,
,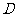 为
为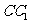 的中点,
的中点,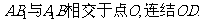
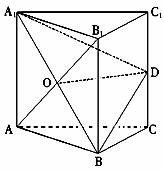
(Ⅰ)求证: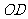 ∥
∥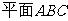
(Ⅱ)求证: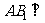 平面
平面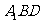 .
.
17.(本小题满分12分)
已知函数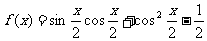 .
.
(Ⅰ)若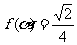 ,
,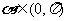 ,求
,求 的值;
的值;
(Ⅱ)求函数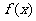 在
在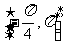 上最大值和最小值.
上最大值和最小值.
16.对于以下四个命题:
①若函数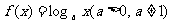 在其定义域内是减函数,则
在其定义域内是减函数,则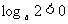 ;
;
②设函数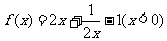 ,则函数
,则函数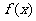 有最小值1;
有最小值1;
③若向量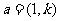 ,
,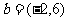 ,
,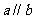 ,则
,则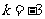 ;
;
④函数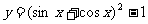 的最小正周期是
的最小正周期是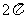 .
.
其中正确命题的序号是______________.
14.已知点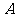 是直角三角形
是直角三角形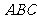 的直角顶点,且
的直角顶点,且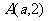 ,
,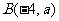 ,
,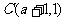 ,则三角形
,则三角形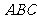 的外接圆的方程是
.
的外接圆的方程是
.
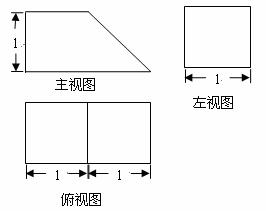
13.一几何体的三视图如下,它的体积为 .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com