
4.根据甲、乙两名篮球运动员某赛季9场比赛得分的茎叶图,可知( )
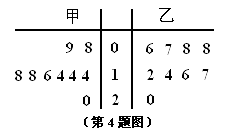
A.甲运动员的成绩好,乙运动员发挥稳定
B.乙运动员的成绩好,甲运动员发挥稳定
C.甲运动员的成绩好,且发挥更稳定
D.乙运动员的成绩好,且发挥更稳定
3.已知两点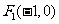 、
、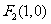 ,且
,且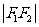 是
是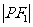 与
与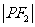 的等差中项,则动点
的等差中项,则动点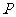 的轨迹方程是 ( )
的轨迹方程是 ( )
A.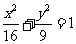 B.
B.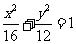 C.
C.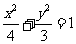 D.
D.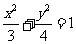
2. 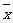 是
是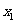 ,
,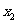 ,
, ,
,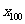 的平均数,
的平均数,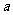 是
是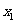 ,
,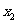 ,
, ,
,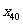 的平均数,
的平均数,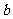 是
是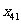 ,
,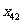 ,
, ,
,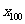 的平均数,则下列各式中正确的是 ( )
的平均数,则下列各式中正确的是 ( )
A.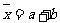 B.
B.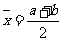 C.
C.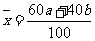 D.
D.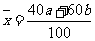
1.从装有两个红球和两个黑球的口袋内任取两个球,那么互斥而不对立的两个事件是( )
A.“至少有一个黑球”与“都是黑球” B.“至少有一个黑球”与“至少有一个红球”
C.“恰有一个黑球”与“恰有两个黑球” D.“至少有一个黑球”与“都是红球”
22.双曲线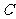 的中心在原点,右焦点为
的中心在原点,右焦点为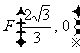 ,渐近线方程为
,渐近线方程为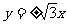 .
.
(Ⅰ)求双曲线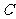 的方程;
的方程;
(Ⅱ)设直线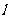 :
: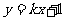 与双曲线
与双曲线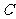 交于
交于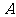 、
、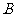 两点,问:
两点,问:
① 当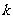 为何值时,以
为何值时,以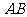 为直径的圆过原点;
为直径的圆过原点;
② 是否存在实数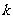 ,使
,使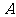 、
、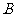 两点关于直线
两点关于直线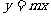 对称(
对称(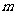 为常数).若存在,求出
为常数).若存在,求出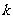 的值;若不存在,说明理由.
的值;若不存在,说明理由.
21.已知动点P与平面上两点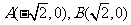 连线的斜率的积为
连线的斜率的积为 .
.
(Ⅰ)求动点P的轨迹方程.
(Ⅱ)设直线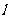 经过点(0,1),与点P的轨迹交于两点M、N,当|MN|=
经过点(0,1),与点P的轨迹交于两点M、N,当|MN|=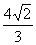 时,求直线l的方程.
时,求直线l的方程.
20.若点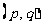 在
在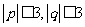 表示的区域中均匀随机出现,求关于x的方程
表示的区域中均匀随机出现,求关于x的方程
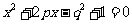 有两个实数根的概率.
有两个实数根的概率.
19.已知命题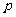 :关于x的方程
:关于x的方程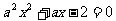 在[-1,1]上有解. 命题
在[-1,1]上有解. 命题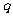 :只有一个实数
:只有一个实数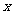 满足不等式
满足不等式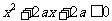 . 若命题“p或q”是假命题,求实数a的取值范围.
. 若命题“p或q”是假命题,求实数a的取值范围.
18.冰箱里有5袋牛奶,其中有两袋已经过期,小明随机取出两袋牛奶. 求:
(Ⅰ)两袋牛奶都已过期的概率;
(Ⅱ)至少有一袋过期牛奶的概率.
17.已知双曲线与椭圆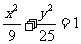 有相同的焦点,且离心率之和为
有相同的焦点,且离心率之和为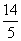 ,求双曲线的方程.
,求双曲线的方程.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com