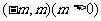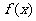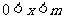22．已知定义在区间上，值域为R的函数满足：①当时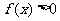；②对于定义域内任意的实数a, b均满足：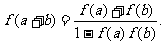

(1)试求；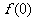

(2)判断并证明函数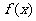的单调性；

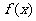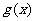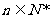(3)若函数存在反函数，当时，

求证：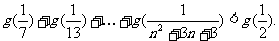

21．已知函数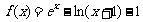

(1)求函数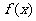的单调区间及最小值；

(2)当集合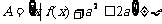时，解关于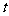的不等式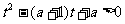

20．水库的蓄水量随时间而变化。现用t表示时间，以月为单位，年初为起点，根据历年数据，某水库的蓄水量(单位：亿立方米)关于t的近似函数关系式为

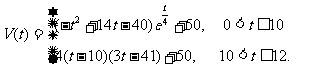
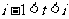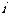(1)该水库的蓄水量小于50的时期称为枯水期。以表示第月份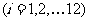,问一年内哪几个月份是枯水期？

(2)求一年内该水库的最大蓄水量(取e=2.7计算)。

19．已知函数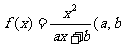为常数)且方程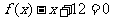有两个实根为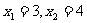

(1)求函数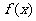的解析式；

(2)设k>1，解关于x的不等式：.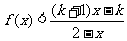

18．某项考试按科目A、科目B依次进行，只有当科目A成绩合格时，才可继续参加科目B的考试。已知每个科目只允许有一次补考机会，两个科目成绩均合格方可获得证书。现某人参加这项考试，科目A每次考试成绩合格的概率均为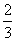，科目B每次考试成绩合格的概率均为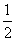。假设各次考试成绩合格与否均互不影响.

(1)求他不需要补考就可获得证书的概率；

(2)在这项考试过程中，假设他不放弃所有的考试机会，记他参加考试的次数为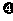，求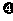的数学期望E.

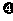17．奇函数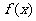在其定义域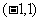上单调递增，且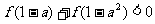，求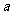的取值范围.

16．函数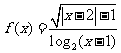的定义域为　　　　　 ．

15．已知函数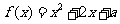,,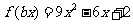其中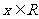,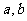为常数，则方程的解集为　　　　　　 .　

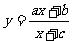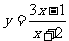14．已知函数的反函数是，则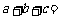　 　

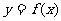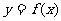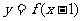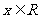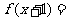
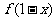13．对于定义在R上的函数有下述四个命题：1若是奇函数，则的图象关于点A(1,0)对称；2若对于任意都有，则函数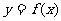的图象关于直线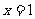对称；3若函数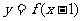的图象关于直线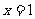对称，则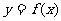为偶函数；4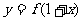函数与函数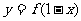的图象关于直线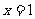对称。

中正确命题的序号为　　　　　　　 (把你认为正确的命题的序号都填上)