20．(12分)某出租车租赁公司拥有汽车100辆,拟对外出租,当每辆车的月租金为3000元时,可全部租出．当每辆车的月租金每增加50元时,未租出的车将会增加一辆,租出的车公司每辆每月需付维护费150元,未租出的车公司每辆每月需付维护费50元．

(1)当每辆车的月租金定为3600元时,能租出多少辆车?

(2)当每辆车的月租金定为多少元时,租赁公司的月收益最大?最大月收益是多少?

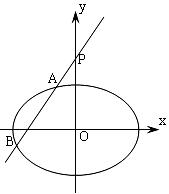
19．(12分)已知椭圆 +=1 ,过点P(0,3)作直线l顺次交椭圆于A、B两点,以线段AB为直径作圆．试问该圆能否经过原点?若能,求出此时的直线l的方程;若不能,请说明理由．

18．(12分)已知函数f(x)=2sinx·cosx- 2cos²x+ +b ．

(1)　　 当x∈R,写出函数f(x)的单调递减区间;

(2)　　 设x∈[0,],f(x)的最小值是-2,求实数b的值．

17．(12分)已知二次函数f(x)=x²-4ax+2a+6 (a∈R)．

(1)若对x∈R,都有f(2-x)=f(2+x),求函数f(x)在[0,3]上的最小值和最大值;

(2)若函数f(x)的值域为[0,+∞),且a＞0,求函数g(x)=log_a(x²-2x-3)的减区间．

16．设ab＞0,直线ax+by-1=0过点(2,1),u= + 的最小值为　　　　　

15．幂函数f(x)=x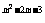 (m∈Z)为偶函数,且在区间(0,+∞)上是单调递减函数,则m=　　

14．设{a_n}是公比q＞1的等比数列,若a₂₀₀₄和a₂₀₀₅是方程4x²-8x+3=0的两根,则a₂₀₀₆+a₂₀₀₇=

13．若cos(α+β)=,cos(α-β)=,则tanα·tanβ=　　　　　　

12．已知F₁、F₂是椭圆的两个焦点,过F₁且与椭圆长轴垂直的直线交椭圆于A、B两点,若△

ABF₂是正三角形,则这个椭圆的离心率是　　　　　

A． 　　　　　　B． 　　　　　C． 　　　　　　D． 　

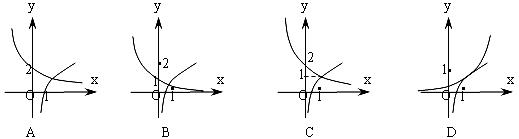
11．函数f(x)=1+log₂x 与g(x)=2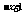在同一直角坐标系下的图象大致是如图中的