
6.椭圆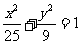 上一点
上一点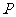 到左焦点的距离为8,那么点
到左焦点的距离为8,那么点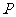 到右准线的距离是 ( )
到右准线的距离是 ( )
A.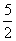 B.
B.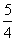 C.
C.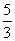 D.
D.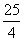
5.若双曲线的焦点为(0,4)和(0, ),虚轴长为
),虚轴长为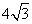 ,则双曲线的方程为 ( )
,则双曲线的方程为 ( )
A.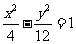 B.
B.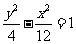 C.
C.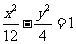 D.
D.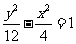
4.根据甲、乙两名篮球运动员某赛季9场比赛得分的茎叶图,可知( )
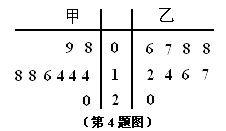
A.甲运动员的成绩好,乙运动员发挥稳定
B.乙运动员的成绩好,甲运动员发挥稳定
C.甲运动员的成绩好,且发挥更稳定
D.乙运动员的成绩好,且发挥更稳定
3.已知两点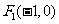 、
、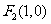 , 且
, 且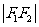 是
是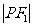 与
与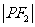 的等差中项,则动点P的轨迹方程是 ( )
的等差中项,则动点P的轨迹方程是 ( )
A.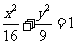 B.
B.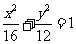 C.
C.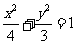 D.
D.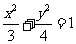
2.若2,4,m,7,8的平均数为6,则m等于 ( )
A.6 B.7 C.8 D.9
1.从装有两个红球和两个黑球的口袋内任取两个球,下列事件中互斥的两个事件是( )
A.“至少有一个黑球”与“都是黑球”
B.“至少有一个黑球”与“至少有一个红球”
C.“恰有一个黑球”与“恰有两个黑球”
D.“至少有一个红球”与“都是红球”
22.(14分)设函数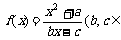 N*),若方程f(x)=x的根为0和2,且
N*),若方程f(x)=x的根为0和2,且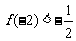 .
.
(1)求函数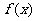 的解析式;
的解析式;
(2)如果各项均不为1且不为零的数列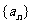 的前n项和为Sn且满足
的前n项和为Sn且满足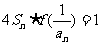 ,
,
求该数列的通项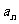 ;
;
(3)如果数列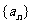 满足
满足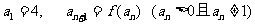 ,问:是否存在正数M,使得:当
,问:是否存在正数M,使得:当 时,恒有
时,恒有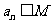 成立?若存在,求出M的取值范围;若不存在,说明理由.
成立?若存在,求出M的取值范围;若不存在,说明理由.
21、(12分)已知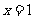 是函数
是函数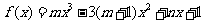 的一个极值点,其中
的一个极值点,其中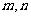 为实数,
为实数,
(1)当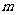 =-2时,求函数
=-2时,求函数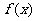 的单调递减区间;
的单调递减区间;
(2)若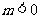 ,当
,当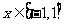 时,函数
时,函数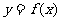 的图象上任意一点的切线斜率恒大于3
的图象上任意一点的切线斜率恒大于3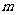 ,求
,求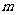 的取值范围.
的取值范围.
20、(12分)已知向量=(cos, sin ),=(cos,–sin),且x∈[0,],
(1)求:·及|+|;
(2)若f(x)=·–2λ|+|的最小值是 –,求λ的值。
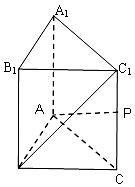
19. (12分)如图,直三棱柱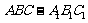 中,AB=2,AC=3,
中,AB=2,AC=3, 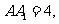
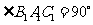 ,
,
(1)求直线BC1与平面ABB1A1所成角的正切值;
(2)P为棱CC1上的动点,当B1C⊥AP时,求CP的长。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com