
5.下列函数中,值域为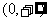 的是
的是
A.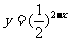 B.
B.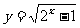 C.
C.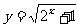 D.
D.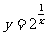
4.下列函数既是奇函数,又在区间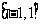 上单调递减的是
上单调递减的是
A.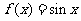 B.
B.
C.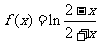 D.
D.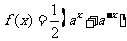
3.若函数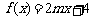 在
在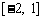 上存在x0,使f (x0)=0,则实数m的取值范围
上存在x0,使f (x0)=0,则实数m的取值范围
A.[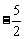 ,4] B.[-2,1]
,4] B.[-2,1]
C.[-1,2] D.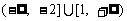
2.设等差数列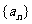 的前n项和是
的前n项和是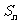 ,
,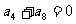 ,则
,则
A.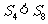 B.
B.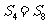 C.
C.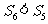 D.
D.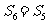
1.若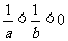 ,则下列结论不正确的是
,则下列结论不正确的是
A.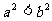 B.
B.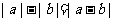 C.
C.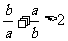 D.
D.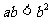
22. (本小题14分)
F1、F2为双曲线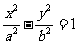 的左右焦点,O为坐标原点,P在双曲线的左支上,点M在右准线上,且满足:
的左右焦点,O为坐标原点,P在双曲线的左支上,点M在右准线上,且满足: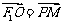 ,
,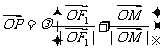 (λ>0)
(λ>0)
(1)求此双曲线的离心率;
(2)若过点N(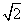 ,
,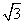 )的双曲线C的虚轴端点分别为B1、B2(B1在y轴正半轴上),点A、B在双曲线上,且
)的双曲线C的虚轴端点分别为B1、B2(B1在y轴正半轴上),点A、B在双曲线上,且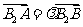 ,
,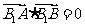 ,求双曲线C和直线AB的方程.
,求双曲线C和直线AB的方程.
21. (本小题14分)
椭圆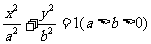 的离心率
的离心率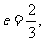 A、B是椭圆上关于x、y轴均不对称的两点,线段AB的垂直平分线与x轴交于点P(1,0).
A、B是椭圆上关于x、y轴均不对称的两点,线段AB的垂直平分线与x轴交于点P(1,0).
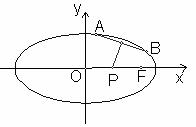
(1)设AB的中点为C(x0,y0),求x0的值;
(2)若F是椭圆的右焦点,且|AF|+|BF|=3,求椭圆的方程.
20. (本小题12分)
已知等差数列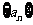 的前9项和为153.
的前9项和为153.
(1)若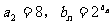 ,求数列
,求数列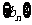 前n项的积
前n项的积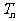 ;
;
(2)在(1)的条件下,若从数列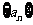 中,依次取出第二项、第四项、第八项,…,第
中,依次取出第二项、第四项、第八项,…,第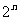 项,按原来的顺序组成一个新的数列
项,按原来的顺序组成一个新的数列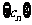 ,求数列
,求数列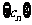 的前n项和
的前n项和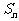 .
.
19. (本小题12分)
已知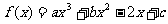 在
在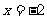 时有极大值6,在
时有极大值6,在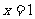 时有极小值,求
时有极小值,求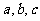 的值;并求
的值;并求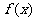 在区间[-3,3]上的最大值和最小值.
在区间[-3,3]上的最大值和最小值.
18.(本小题12分)
在一次招聘面试中,备有10道题,甲能答对其中的6道题,乙能答对其中的8道题,规定每人分别从10道题中随机抽取3道题测试(答完放回),若至少答对2道题者合格.
(1)求甲乙两人至少有一人测试合格的概率;
(2)求甲乙两人中恰有一人测试合格的概率.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com