
4.(08年福建) 设集合A={x|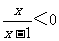 },B={x|0<x<3=,那么“m
},B={x|0<x<3=,那么“m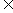 A”是“m
A”是“m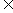 B”的( )
B”的( )
A.充分而不必要条件 B.必要而不充分条件
C.充要条件 D.既不充分也不必要条件
3.(08年北京)已知全集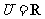 ,集合
,集合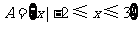 ,
,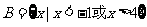 ,那么集合
,那么集合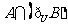 等于
( )
等于
( )
A.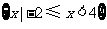 B.
B.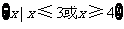 C.
C.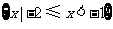 D.
D.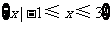
3.(08年北京文)若集合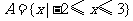 ,
,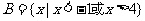 ,则集合
,则集合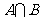 等于
( )
等于
( )
A.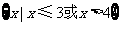 B.
B.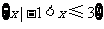
C.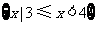 D.
D.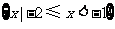
2.设A、B是两个集合,定义A-B={x|x∈A,且x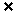 B},若M={x||x+1|≤2},N={x|x=|sinα|,α∈R},则M-N=
( )
B},若M={x||x+1|≤2},N={x|x=|sinα|,α∈R},则M-N=
( )
A.[-3,1] B.[-3,0] C.[0,1] D.[-3,0]
1.设集合P={3,4,5},Q={4,5,6,7},定义P※Q={(a,b)|a∈P,b∈Q},则P※Q中元素的个数为 ( )
A.3 B.4 C.7 D.12
22、(本题满分16分,第1小题8分,第2小题8分)
设函数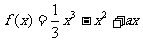 ,
,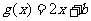 ,当
,当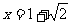 时,
时,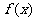 取得极值。
取得极值。
(1) 求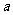 的值,并判断
的值,并判断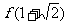 是函数
是函数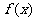 的极大值还是极小值;
的极大值还是极小值;
(2) 当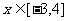 时,函数
时,函数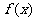 与
与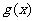 的图象有两个公共点,求
的图象有两个公共点,求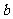 的取值范围。
的取值范围。
21、(本题满分14分,第1小题5分,第2小题9分)
如图,椭圆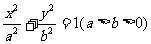 的左、右焦点为
的左、右焦点为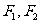 ,过
,过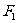 的直线
的直线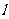 与椭圆相交于
与椭圆相交于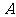 、
、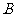 两点。
两点。
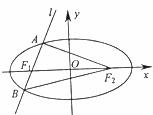
(1) 若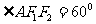 ,且
,且 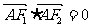 求椭圆的离心率。
求椭圆的离心率。
(2) 若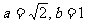 ,求
,求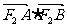 的最大值和最小值。
的最大值和最小值。
20、(本题满分14分,第1小题4分,第2小题5分,第3小题5分)
已知各项均为正数的数列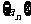 中,
中,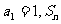 是数列
是数列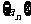 的前
的前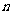 项和,对任意
项和,对任意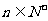 ,有
,有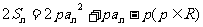
(1) 求常数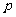 的值;
的值;
(2) 求数列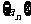 的通项公式;
的通项公式;
(3) 记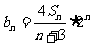 ,求数列
,求数列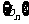 的前
的前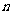 项和
项和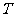 。
。
19、(本题满分12分,第1小题3分,第2小题4分,第3小题5分)
如图,在四棱锥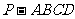 中,ABCD是矩形,
中,ABCD是矩形, ,
,
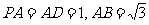 ,点
,点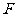 是
是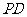 的中点,点
的中点,点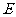 在
在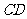 上移动。
上移动。
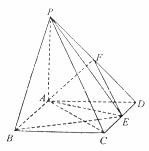
(1) 求三棱锥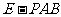 体积;
体积;
(2) 当点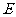 为
为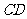 的中点时,试判断
的中点时,试判断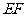 与平面
与平面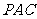 的关系,并说明理由;
的关系,并说明理由;
(3) 求证: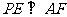
18、(本题满分12分)
要建一间地面面积为20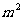 ,墙高为
,墙高为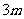 的长方形储藏室,在四面墙中有一面安装一扇门(门的面积和墙面的面积按一定的比例设计)。已知含门一面的平均造价为300元
的长方形储藏室,在四面墙中有一面安装一扇门(门的面积和墙面的面积按一定的比例设计)。已知含门一面的平均造价为300元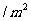 ,其余三面的造价为200元
,其余三面的造价为200元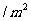 ,屋顶的造价为250元
,屋顶的造价为250元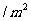 。问怎样设计储藏室地面矩形的长与宽,能使总价最低,最低造价是多少?
。问怎样设计储藏室地面矩形的长与宽,能使总价最低,最低造价是多少?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com