
3.若函数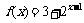 的反函数的图象过P点,则P点坐标可能是 ( )
的反函数的图象过P点,则P点坐标可能是 ( )
A (2,5) B
(2,5) B (1,3)
C
(1,3)
C (5,2) D
(5,2) D (3,1)
(3,1)
2.若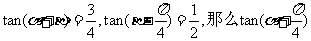 的值等于:( )
的值等于:( )
A.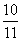 B.
B.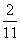 C.
C.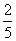 D.2
D.2
1.“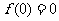 ”是
”是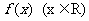 是奇函数的( )条件:
是奇函数的( )条件:
A.充分不必要 B.必要不充分
C.充要 D.非充分非必要
21.(本小题满分14分)已知数列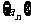 的首项
的首项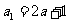 (a是常数,且
(a是常数,且 ),
), (
(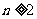 ),数列
),数列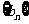 的首项
的首项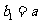 ,
,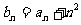 (
(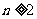 )。
)。
(1)证明: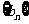 从第2项起是以2为公比的等比数列;
从第2项起是以2为公比的等比数列;
(2)设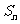 为数列
为数列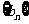 的前n项和,且
的前n项和,且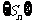 是等比数列,求实数
是等比数列,求实数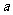 的值;
的值;
(3)当a>0时,求数列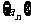 的最小项。
的最小项。
20.(本小题满分13分)设函数f(x)=ax3-2bx2+cx+4d(a, b, c, d∈R)的图象关于原点对称,且x=1时,f(x)取极小值-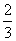 ,
,
(1)求a,b,c,d的值
(2)当x∈[-1,1]时,f(x)图象上是否存在两点,使得过此两点处的切线互相垂直?试证明你的结论
(3)若x1,x2∈[-1,1]时,求证|f(x1)-f(x2)|≤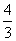 .
.
19.(本题满分12分)已知向量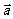 =(cos
=(cos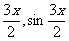 ),
), 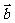 =(cos
=(cos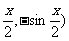 ,x∈[
,x∈[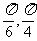 ],
],
(1)求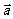 ·
·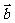 及|
及|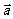 +
+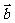 |;
|;
(2)求函数f(x)=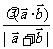 (
(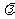 ∈R且
∈R且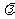 ≠0)的最小值.
≠0)的最小值.
18.(本题满分12分)如图,直二面角D-AB-E中,四边形ABCD是边长为2的正方形,AE=EB,F为CE上的点,且BF⊥平面ACE.
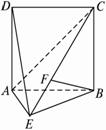
(1)求证:AE⊥平面BCE;
(2)求二面角B-AC-E的大小;
(3)求点D到平面ACE的距离.
17. (本题满分12分)
一个口袋内装有大小相同且已编有不同号码的6个黑球和4个红球,某人一次从中摸出
2个球
(I)如果摸到的球中含有红球就中奖,那么此人中奖的概率是多少?
(II)如果摸到的2个球都是红球,那么就中大奖,在有放回的3次摸球中,此人恰好两次中大奖的概率是多少?
16.(本题满分12分)
若函数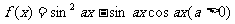 的图像与直线
的图像与直线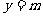 相切,并且切点的横坐标依次成公差为
相切,并且切点的横坐标依次成公差为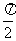 的等差数列.
的等差数列.
(Ⅰ)求m的值;
(Ⅱ)若点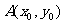 是
是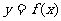 图像的对称中心,且
图像的对称中心,且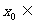 [0,
[0,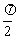 ],求点A的坐标.
],求点A的坐标.
15.定义运算符号:“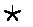 ”,这个符号表示若干个数相乘,例如:可将1×2×3×…×n记作
”,这个符号表示若干个数相乘,例如:可将1×2×3×…×n记作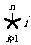 ,
,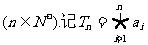 ,其中ai为数列
,其中ai为数列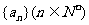 中的第i项.
中的第i项.
①若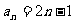 ,则T4=
;
,则T4=
;
②若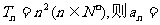 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com