
22.(本小题满分12分)(理) 设函数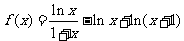 .
.
(Ⅰ)求f(x)的单调区间和极值;
(Ⅱ)是否存在实数a,使得关于x的不等式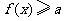 的解集为(0,+
的解集为(0,+ )?若存在,求a的取值范围;若不存在,试说明理由.
)?若存在,求a的取值范围;若不存在,试说明理由.
(文) 已知常数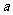 、
、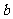 、
、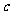 都是实数,函数
都是实数,函数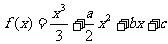 的导函数为
的导函数为
(Ⅰ)设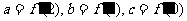 ,求函数
,求函数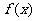 的解析式;
的解析式;
(Ⅱ)如果方程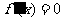 的两个实数根分别为
的两个实数根分别为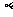 、
、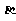 ,并且
,并且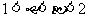
问:是否存在正整数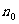 ,使得
,使得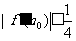 ?请说明理由.
?请说明理由.
21.(本小题满分12分)(理)已知奇函数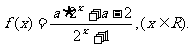
(Ⅰ)试确定实数a的值,并证明f(x)为R上的增函数;
(Ⅱ)记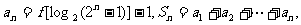 求
求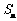 ;
;
(Ⅲ)若方程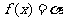 在(-∞,0)上有解,试证
在(-∞,0)上有解,试证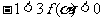
(文)数列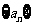 :满足
:满足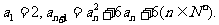
(Ⅰ)
设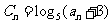 ,求证
,求证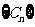 是等比数列;
是等比数列;
(Ⅱ)
求数列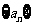 的通项公式;
的通项公式;
(Ⅲ)设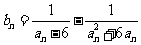 ,数列
,数列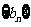 的前
的前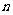 项和为
项和为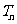 ,求证:
,求证: 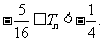
20.(本小题满分12分)已知函数f(x)的定义域为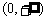 ,且对任意的正实数x、y都有f(xy)=f(x)+f(y),且当x>1时,f(x)>0,f(4)=1.
,且对任意的正实数x、y都有f(xy)=f(x)+f(y),且当x>1时,f(x)>0,f(4)=1.
(1)求证:f(1)=0;
(2)求: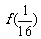 ;
;
(3)解不等式:f(x)+f(x-3)≤1.
19.(本小题满分12分)在数列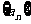 中,
中,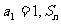 表示该数列的前n项和.若已知
表示该数列的前n项和.若已知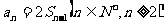
(1)求证:数列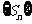 是等比数列;
是等比数列;
(2)求数列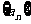 的通项公式.
的通项公式.
18.(本小题满分12分).
一个不透明的口袋内装有材质、重量、大小相同的7个小球,且每个小球的球面上要么只写有数字“08”,要么只写有文字“奥运”.假定每个小球每一次被取出的机会都相同,又知从中摸出2个球都写着“奥运”的概率是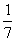 。现甲、乙两个小朋友做游戏,方法是:不放回从口袋中轮流摸取一个球,甲先取、乙后取,然后甲再取,直到两个小朋友中有1人取得写着文字“奥运”的球时游戏终止,每个球在每一次被取出的机会均相同.
。现甲、乙两个小朋友做游戏,方法是:不放回从口袋中轮流摸取一个球,甲先取、乙后取,然后甲再取,直到两个小朋友中有1人取得写着文字“奥运”的球时游戏终止,每个球在每一次被取出的机会均相同.
(1)求该口袋内装有写着数字“08”的球的个数;
(2)求当游戏终止时总球次数不多于3的概率.
17.(本小题满分10分)已知集合A={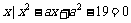 },B=
},B=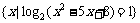 ,C=
,C=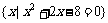 ,若
,若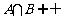 与
与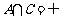 同时成立,求实数a的值。
同时成立,求实数a的值。
16.已知函数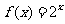 ,等差数列
,等差数列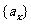 的公差为
的公差为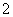 .若
.若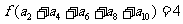 ,则
,则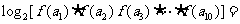 .
.
15.曲线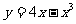 在点
在点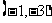 处的切线方程是
.
处的切线方程是
.
14.已知函数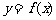 是定义在R上的奇函数,且
是定义在R上的奇函数,且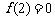 ,对任意
,对任意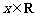 ,都有
,都有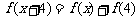 成立,则
成立,则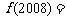 ______.
______.
13.函数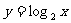 与函数
与函数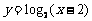 的图象及
的图象及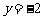 与
与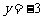 所围成的图形面积是
所围成的图形面积是
__ __.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com