
7.已知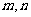 是两条不同直线,
是两条不同直线,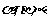 是三个不同平面,下列命题中正确的是( )
是三个不同平面,下列命题中正确的是( )
A.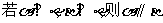 B.
B.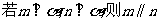
C.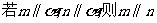 D.
D.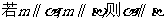
6.正四棱锥的侧棱长为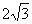 ,侧棱与底面所成的角为
,侧棱与底面所成的角为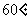 ,则该棱锥的体积为( )
,则该棱锥的体积为( )
A.3 B.6 C.9 D.18
5.某班级要从4名男生、2名女生中选派4人参加某次社区服务,如果要求至少有1名女生,那么不同的选派方案种数为( )
A.14 B.24 C.28 D.48
4.若 展开式的二项式系数之和为64,则展开式的常数项为( )
展开式的二项式系数之和为64,则展开式的常数项为( )
A.10 B.20 C.30 D.120
3.某一批花生种子,如果每1粒发芽的概率为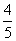 ,那么播下3粒种子恰有2粒发芽的概率是( )
,那么播下3粒种子恰有2粒发芽的概率是( )
A.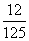 B.
B.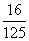 C.
C.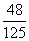 D.
D.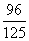
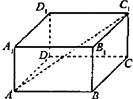
2.如图,在长方体ABCD-A1B1C1D1中,AB=BC=2,AA1=1,则AC1与平面A1B1C1D1所成角的正弦值为( )
A.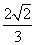 B.
B.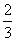 C.
C.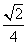 D.
D.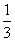
1. 一物体的运动方程为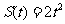 (位移单位:米,时间单位:秒),则该物体在1秒时的瞬时速度为(
)
(位移单位:米,时间单位:秒),则该物体在1秒时的瞬时速度为(
)
A.1米/秒 B. 2米/秒 C. 3米/秒 D.4米/秒
21.(本小题满分14分) 7、9、10班同学做乙题,其他班同学任选一题,若两题都做,则以较少得分计入总分.
(甲)已知f(x)=ax-ln(-x),x∈[-e,0),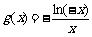 ,其中e=2.718 28…是自然对数的底数,a∈R.
,其中e=2.718 28…是自然对数的底数,a∈R.
(1)若a=-1,求f(x)的极值;
(2)求证:在(1)的条件下,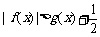 ;
;
(3)是否存在实数a,使f(x)的最小值是3,如果存在,求出a的值;如果不存在,说明理由.
(乙)定义在(0,+∞)上的函数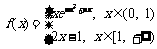 ,其中e=2.718 28…是自然对数的底数,a∈R.
,其中e=2.718 28…是自然对数的底数,a∈R.
(1)若函数f(x)在点x=1处连续,求a的值;
(2)若函数f(x)为(0,1)上的单调函数,求实数a的取值范围;并判断此时函数f(x)在(0,+∞)上是否为单调函数;
(3)当x∈(0,1)时,记g(x)=lnf(x)+x2-ax. 试证明:对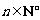 ,当n≥2时,有
,当n≥2时,有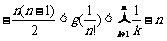
20.(本小题满分13分) 由坐标原点O向函数y=x3 -3x2的图象W引切线l1,切点P1(x1,y1) (P1,O不重合),再由点P1引W的切线l2,切点为P2(x2,y2) (P1, P2不重合),…,如此继续下去得到点列{Pn(xn,yn)}.
(1)求x1的值;
(2)求xn与xn+1满足的关系式;
(3)求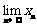 的值。
的值。
19.(本题满分12分)如图,某地有三家工厂,分别位于矩形ABCD 的顶点A、B 及CD的中点P 处,已知AB=20km,CB =10km ,为了处理三家工厂的污水,现要在矩形ABCD 的区域上(含边界),且与A、B等距离的一点O处建造一个污水处理厂,并铺设排污管道AO、BO、OP ,设排污管道的总长度为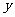 km.
km.
(1)按下列要求写出函数关系式:
①设∠BAO=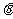 (rad),将
(rad),将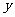 表示成
表示成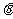 的函数;②设OP
的函数;②设OP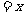 (km) ,将
(km) ,将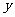 表示成
表示成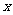 的函数.
的函数.
(2)请选用(1)中的一个函数关系式,确定污水处理厂的位置,使铺设的排污管道总长度最短.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com