
1.用反证法证明命题“若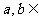 N
N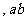 可被
可被 整除,那么
整除,那么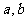 中至少有一个能被
中至少有一个能被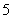 整除”.那么假设的内容是
整除”.那么假设的内容是
A.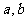 都能被
都能被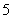 整除
B.
整除
B.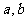 都不能被
都不能被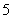 整除
整除
C.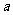
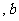 有一个能被
有一个能被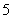 整除 D.
整除 D.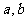 有一个不能被
有一个不能被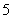 整除
整除
22.(本小题共14分)
设函数 ,其中
,其中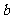 为常数.
为常数.
(1)当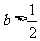 时,判断函数
时,判断函数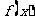 在定义域上的单调性;
在定义域上的单调性;
(2)若函数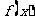 有极值点,求
有极值点,求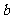 的取值范围及
的取值范围及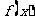 的极值点.
的极值点.
21.(本小题共12分)
若函数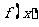 对于定义域中的任意实数
对于定义域中的任意实数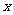 ,都存在实常数
,都存在实常数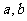 满足
满足
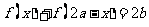 ,则称
,则称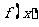 关于点
关于点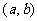 对称.
对称.
(1)已知函数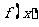
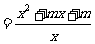 的图象关于
的图象关于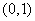 对称,求实数
对称,求实数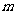 的值;
的值;
(2)在(1)的结论下,已知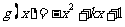 ,若对于任意的正实数
,若对于任意的正实数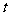 和负实数
和负实数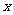 ,恒有
,恒有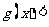
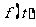 成立,求实数
成立,求实数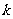 的取值范围.
的取值范围.
20.(本小题共12分)
命题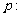 实数
实数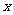 满足
满足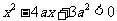 ,其中
,其中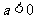 ,命题
,命题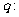 实数
实数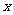 满足
满足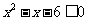 或
或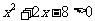 ,且
,且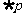 是
是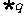 的必要不充分条件,求
的必要不充分条件,求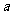 的取值范围.
的取值范围.
19.(本小题共12分)
某汽车生产企业上半年生产汽车的投入成本为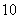 万元/辆,出厂价为
万元/辆,出厂价为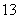 万元/辆,年销售量为
万元/辆,年销售量为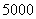 辆.本年度为适应市场的需求,计划提高产品的档次,适当增加成本,若每辆车投入成本增加的比例为
辆.本年度为适应市场的需求,计划提高产品的档次,适当增加成本,若每辆车投入成本增加的比例为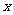 (
(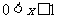 ),则出厂价相应提高的比例为
),则出厂价相应提高的比例为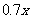 ,年销售量也相应地增加,已知年利润=(每辆车的出厂价-每辆车的投入成本)
,年销售量也相应地增加,已知年利润=(每辆车的出厂价-每辆车的投入成本)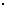 年销售量.
年销售量.
(1)若年销售量增加的比例为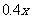 ,为使本年度的年利润比上年度有所增加,则投入成本增加的比例
,为使本年度的年利润比上年度有所增加,则投入成本增加的比例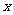 应在什么范围内?
应在什么范围内?
(2)若年销售量关于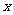 的函数为
的函数为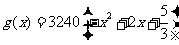 ,则当
,则当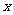 为何值时,本年度的利润最大?最大利润为多少?
为何值时,本年度的利润最大?最大利润为多少?
18.(本小题共12分)
已知实数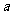 、
、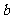 、
、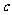 满足
满足 ,
,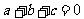 .
.
(1)求证:关于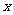 的方程
的方程 有一个正实根和一个负实根;
有一个正实根和一个负实根;
(2)证明: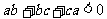 .
.
17.(本小题共12分)
某工厂对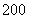 个电子元件的使用寿命进行检查,按照使用寿命,可以把这批电子元件分成第一组
个电子元件的使用寿命进行检查,按照使用寿命,可以把这批电子元件分成第一组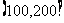 ,第二组
,第二组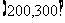 ,第三组
,第三组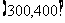 ,第四组
,第四组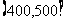 ,第五组
,第五组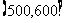 ,第六组
,第六组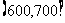 ,由于工作不慎将部分数据丢失,现有以下图表.
,由于工作不慎将部分数据丢失,现有以下图表.

(1)求图2中的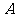 及表格中的
及表格中的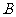 ,
,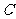 ,
,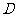 ,
,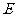 ,
,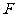 ,
,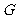 ,
,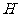 ,
,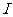 的值;
的值;
(2)求上图中阴影部分的面积;
(3)若电子元件的使用时间超过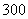
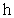 ,则为合格产品,求这批电子元件合格的概率.
,则为合格产品,求这批电子元件合格的概率.
16.将全体正整数排成一个三角形数阵:

按照以上排列的规律,第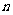 行(
行(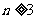 )从左向右的第3个数为 .
)从左向右的第3个数为 .
15.图l是某县参加2008年高考的学生身高条形统计图,从左到右的各条形表示的学生人数依次记为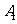 、
、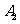 、…、
、…、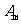 (如
(如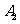 表示身高(单位:
表示身高(单位: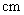 )在[150,155)内的学生人数).图2是统计图l中身高在一定范围内学生人数的一个算法流程图.现要统计身高在160-180
)在[150,155)内的学生人数).图2是统计图l中身高在一定范围内学生人数的一个算法流程图.现要统计身高在160-180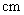 (含160
(含160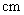 ,不含180
,不含180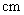 )的学生人数,那么在流程图中的判断框内应填写的条件是
.
)的学生人数,那么在流程图中的判断框内应填写的条件是
.

14.已知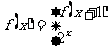
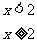 ,则
,则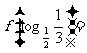 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com